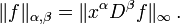Espace de schwartz

Espace de Schwartz

En mathématiques, l'espace 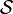${\mathcal S}$ de Schwartz est un espace de fonctions utilisé notamment en théorie des distributions, pour la définition générale de la transformation de Fourier d'une distribution tempérée. La lettre 'S' a été choisie par Schwartz lui même, celui-ci nommant "sphériques" les distributions qu'on appelle de nos jours "tempérées".

Définition

Une fonction f fait partie de l'espace 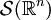$\mathcal{S}(\mathbb{R}^n)$ lorsqu'elle est indéfiniment dérivable, et si f et toutes ses dérivées sont à décroissance rapide, c'est-à-dire que leur produit par une fonction polynôme quelconque est borné.

Pour deux multi-indices $α,β$ on peut noter

$\|f\|_{\alpha,\beta}=\|x^\alpha D^\beta f\|_\infty\,.$

Alors l'espace de Schwartz peut être décrit comme

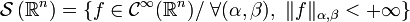$\mathcal{S} \left(\mathbb{R}^n\right) = \{ f \in \mathcal{C}^\infty(\mathbb{R}^n) /\ \forall (\alpha, \beta),\ \|f\|_{\alpha,\beta} < +\infty \}$ .

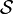
S'il n'y a pas d'ambiguïté, l'espace peut être simplement représenté par la lettre $\mathcal{S}$

Exemples et propriétés

L'espace 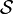$\mathcal{S}$ contient l'espace des fonctions 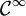$\mathcal{C}^\infty$ à support compact.

Il contient également d'autres éléments comme les fonctions de la forme produit d'un polynôme et d'une gaussienne :

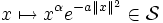$x\mapsto x^\alpha e^{-a \|x\|^2} \in \mathcal{S}$ pour un certain multi-indice α et un réel

a > 0

L'espace 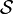$\mathcal{S}$ est un sous-espace vectoriel des différents espaces L^p pour $p\in[1;+\infty]$ .

Il est stable par dérivation, par multiplication ou même par multiplication par un polynôme

Il est dense dans $L 2$ .

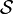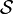La transformation de Fourier est un isomorphisme linéaire de $\mathcal{S}$ dans $\mathcal{S}$ .

Références

L.Schwartz Théorie des distributions et transformation de Fourier Annales de l'Université de Grenoble- T.23, 1948

Portail des mathématiques

Ce document provient de « Espace de Schwartz ».

Catégories : Espace fonctionnel remarquable | Théorie des distributions

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Espace de schwartz de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Espace De Schwartz — En mathématiques, l espace de Schwartz est un espace de fonctions utilisé notamment en théorie des distributions, pour la définition générale de la transformation de Fourier d une distribution tempérée. La lettre S a été choisie par Schwartz lui… … Wikipédia en Français
Espace de Schwartz — En mathématiques, l espace de Schwartz est un espace de fonctions utilisé notamment en théorie des distributions, pour la définition générale de la transformation de Fourier d une distribution tempérée. La lettre S a été choisie par Schwartz lui… … Wikipédia en Français
Espace Fonctionnel — En mathématiques, un espace fonctionnel est un ensemble d applications d une certaine forme d un ensemble X vers un ensembleY. Il est appelé espace parce que suivant les cas il peut être un espace topologique ou un espace vectoriel ou les deux.… … Wikipédia en Français
Espace fonctionnel — En mathématiques, un espace fonctionnel est un ensemble d applications d une certaine forme d un ensemble X vers un ensemble Y. Il est appelé « espace » car, selon les cas, il peut être un espace topologique, un espace vectoriel, ou les … Wikipédia en Français
Espace des fonctions tests — Distribution (mathématiques) Pour les articles homonymes, voir Distribution. En analyse mathématique, une distribution (également appelée fonction généralisée) est un objet qui généralise la notion de fonction et de mesure. La théorie des… … Wikipédia en Français
Schwartz's — Pour les articles homonymes, voir Schwarz. Schwartz s Sandwich à la viande fumée de chez Schwartz s … Wikipédia en Français
Espace propre — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… … Wikipédia en Français
Valeur propre, vecteur propre et espace propre — Fig. 1. A étire le vecteur x sans changer sa direction. x est un vecteur propre pour A, pour la valeur propre λ. En mathématiques, et plus particulièrement en algèbre linéaire, le concept de vecteur propre est une notion algébrique s appliquant à … Wikipédia en Français
Sous-espace propre — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… … Wikipédia en Français
Transformée de Fourier — Joseph Fourier En analyse, la transformation de Fourier est un analogue de la théorie des séries de Fourier pour les fonctions non périodiques, et permet de leur associer un spectre en fréquences. On cherche ensuite à obtenir l expression de la… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Espace de schwartz