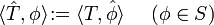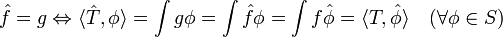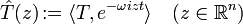Distribution Tempérée

Distribution tempérée

Une distribution tempérée est une distribution T dont le domaine s'étend à $S$ , au sens où T peut alors être identifiée à un élément du dual topologique de S. L'ensemble des distributions tempérées se note naturellement ' S' '.

S' est alors un sous-espace vectoriel (propre) de D' (remarquer: S est plus grand que D, S' est plus petit que D') et il existe un critère simple d'appartenance à S': Si T est à support compact, elle est tempérée. Par exemple, 1 et $δ$ sont tempérées.

Les distributions tempérées ont été introduites par Laurent Schwartz, mais sous l'appellation 'distributions sphériques', ce qui explique l'emploi de la lettre S par Schwartz lui-même!

Sommaire

1 Topologie
2 Transformée de Fourier, cas général
- 2.1 Définition
- 2.2 premières propriétés
3 Cas des distributions tempérées à support compact
- 3.1 Transformée de Fourier-Laplace
4 Application aux équations différentielles
5 Références

Topologie

La topologie de S' est évidemment sa topologie faible-*. (S' est localement convexe et son dual topologique s'identifie à S)

Explicitement :

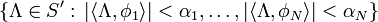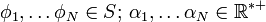La collection de tous les ensembles de la forme $\{\Lambda \in S' :\, | \langle \Lambda , \phi_1 \rangle | < \alpha_1 , \dots, | \langle \Lambda , \phi_N \rangle | < \alpha_N \}$ ( où $\phi_1,\dots \phi_N \in S ; \, \alpha_1,\dots \alpha_N \in \mathbb{R}^{ \ast +}$ ) est une base de voisinages de 0.

Et par suite :

Si U désigne une réunion de tels ouverts, alors tout voisinage de T est de la forme T+U, et les ouverts de S' sont les ensembles T+U.

Ainsi la convergence dans S' est analogue à la convergence au sens des distributions: Dire que la suite ${T N}$ de S' tends vers T signifie que pour toute fonction 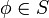$\phi\in S$ , on a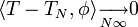 $\langle T-T_N, \phi\rangle\underset{N\infty}{\longrightarrow} 0$

Transformée de Fourier, cas général

Définition

La transformée de Fourier 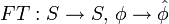$FT: S\rightarrow S , \, \phi \rightarrow \hat{\phi}$ est un de automorphisme $S$ . La généralisation suivante est donc consistante:

$\langle \hat{T}, \phi \rangle\!:= \langle {T}, \hat{\phi} \rangle\ \quad (\phi\in S)$

(On définit bien une distributions tempérée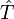 $\hat{T}$ et l'on retrouve la transformée de Fourier usuelle si T s'identifie à une fonction $f\in S$ :

$\hat{f}=g \Leftrightarrow \langle \hat{T}, \phi \rangle = \int g\phi = \int \hat{f} \phi = \int f \hat{\phi}= \langle T, \hat{\phi} \rangle \quad (\forall \phi\in S )$

)

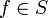Ainsi, transformée de Fourier au sens des distributions est un automorphisme de $S'$ .

premières propriétés

$F T$ est un automorphisme de S, de période 4 (i.e 4 est le plus entier positif k tel que 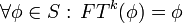$\forall \phi \in S:\, FT^k (\phi)= \phi$ ) , bicontinu ( $F T - 1$ est aussi continue)

On peut montrer que la transformée de Fourier dans S' hérite de ces propriétés.

En particulier 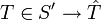$T\in S' \rightarrow \hat{T}$ est continue- ce qui a pour conséquence: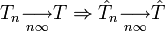

$T_n \underset{n\infty}{\longrightarrow} T \Rightarrow \hat{T}_n \underset{n\infty}{\longrightarrow} \hat{T}$

Cas des distributions tempérées à support compact

Dans cette section, T est à support compact.

On peut montrer que 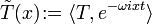$\tilde{T}(x)\!:= \langle T, e^{-\omega ixt} \rangle$ a un sens, du fait de la compacité du support de T.

de plus, 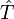$\hat{T}$ s'identifie alors à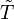 $\tilde{T}$

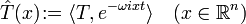
On peut alors poser $\hat{T} (x)\!:= \langle T, e^{-\omega ixt} \rangle \quad (x\in\mathbb{R}^n)$

Transformée de Fourier-Laplace

Donnons maintenant :

$\hat{T} (z)\!:= \langle T, e^{-\omega izt} \rangle \quad (z\in\mathbb{R}^n)$

Ce qui définit la transformée de Fourier-Laplace de T. C'est bien sûr une extension à 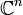$\mathbb{C}^n$ de Fourier.

On montre (théorème de Paley-Wiener) qu'une telle fonction 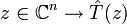$z\in \mathbb{C}^n \rightarrow \hat{T}(z)$ est entière.

Application aux équations différentielles

Références

L.Schwartz, Théorie des distributions et transformation de Fourier, 1948
W.Rudin, Functional Analysis, 1991

Portail des mathématiques

Ce document provient de « Distribution temp%C3%A9r%C3%A9e ».

Catégorie : Théorie des distributions

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Distribution Tempérée de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Distribution tempérée — Une distribution tempérée est une distribution T dont le domaine s étend à l espace de Schwartz , au sens où T peut alors être identifiée à un élément du dual topologique (continu) de . L ensemble des distributions tempérées se note naturellement … Wikipédia en Français
Distribution De Dirac — La distribution de Dirac, aussi appelée par abus de langage fonction δ de Dirac, introduite par Paul Dirac, peut être informellement considérée comme une fonction δ qui prend une « valeur » infinie en 0, et la valeur zéro partout… … Wikipédia en Français
Distribution de dirac — La distribution de Dirac, aussi appelée par abus de langage fonction δ de Dirac, introduite par Paul Dirac, peut être informellement considérée comme une fonction δ qui prend une « valeur » infinie en 0, et la valeur zéro partout… … Wikipédia en Français
Distribution (Biologie) — Aire de répartition L’aire de répartition, appelée aussi aire de distribution ou simplement distribution, est la zone délimitant la répartition géographique d une espèce vivante ou de toute autre unité taxonomique qui inclut la totalité de ses… … Wikipédia en Français
Distribution (biologie) — Aire de répartition L’aire de répartition, appelée aussi aire de distribution ou simplement distribution, est la zone délimitant la répartition géographique d une espèce vivante ou de toute autre unité taxonomique qui inclut la totalité de ses… … Wikipédia en Français
Distribution de Dirac — La distribution de Dirac, aussi appelée par abus de langage fonction δ de Dirac, introduite par Paul Dirac, peut être informellement considérée comme une fonction δ qui prend une « valeur » infinie en 0, et la valeur zéro partout… … Wikipédia en Français
Aire de distribution — Aire de répartition L’aire de répartition, appelée aussi aire de distribution ou simplement distribution, est la zone délimitant la répartition géographique d une espèce vivante ou de toute autre unité taxonomique qui inclut la totalité de ses… … Wikipédia en Français
Transformée de Fourier — Joseph Fourier En analyse, la transformation de Fourier est un analogue de la théorie des séries de Fourier pour les fonctions non périodiques, et permet de leur associer un spectre en fréquences. On cherche ensuite à obtenir l expression de la… … Wikipédia en Français
DÉRIVÉES PARTIELLES (ÉQUATIONS AUX) - Théorie linéaire — Il existe une théorie mathématique assez bien constituée des équations aux dérivées partielles linéaires, dont nous allons essayer de donner une idée. En contraste, les équations non linéaires présentent un foisonnement de problèmes et de… … Encyclopédie Universelle
DISTRIBUTIONS (mathématiques) — Il est arrivé à plusieurs reprises que certaines exigences de la physique, par exemple, aient conduit les utilisateurs des mathématiques à des «calculs» non rigoureusement justifiables au moyen des concepts mathématiques existants, mais qui… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Distribution Tempérée