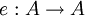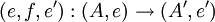- Enveloppe de karoubi
-
Enveloppe de Karoubi
En mathématiques, l’enveloppe de Karoubi d'une catégorie C est une classification des idempotents de C, au moyen d'une catégorie auxiliaire. Elle porte le nom du mathématicien français Max Karoubi.
Sommaire
Définition
Soit une catégorie C, alors un idempotent de C est un endomorphisme :
qui vérifie e2 = e. Son enveloppe de Karoubi, parfois notée Split(C), est une catégorie contenant les paires de la forme (A, e) avec e : A → A un idempotent de C, et des triplets de morphismes de la forme :
avec f : A → A’ un morphisme de C qui vérifie
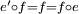 ou, de manière équivalente,
ou, de manière équivalente, 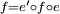 .
.La composition dans Split(C) se fait comme dans C, mais le morphisme identité de (A,e) sur Split(C) est (e,e,e), au lieu de l'identité de A.
La catégorie C est incluse dans Split(C). De plus, dans Split(C), tout idempotent est scindé : pour tout idempotent f : (A,e) → (A’,e’), il existe une paire (g : (A,e) → (A’’,e’’), h : (A’’,e’’) → (A’,e’)) telle que :
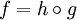 et
et 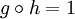 .
.
L'enveloppe de Karoubi d'une catégorie C peut ainsi être considérée comme la « complétion » de C, qui scinde les idempotents.
L'enveloppe de Karoubi d'une catégorie C peut de façon équivalente être définie comme la sous-catégorie pleine de
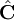 (les préfaisceaux sur C) des rétractée des foncteurs représentables.
(les préfaisceaux sur C) des rétractée des foncteurs représentables.Automorphismes de l'enveloppe de Karoubi
Un automorphisme de Split(C) est de la forme (e, f, e) : (A, e) → (A, e), d'inverse (e, g, e) : (A, e) → (A, e) qui vérifie :
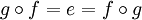 ;
;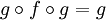 ;
;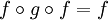 ;
;
Si on se contente, au lieu de la première équation, de la relation
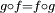 , alors f est un automorphisme partiel, d'inverse g. Une involution (partielle) de Split(C) est un automorphisme (partiel) auto-inverse.
, alors f est un automorphisme partiel, d'inverse g. Une involution (partielle) de Split(C) est un automorphisme (partiel) auto-inverse.Exemple
Si C est muni du produit, alors un isomorphisme f : A → B étant donné, l'application f × f -1 : A × B → B × A, composée avec son application canoniquement symétrique γ : B × A → A × B, est une involution partielle.
Références
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Karoubi envelope ».
- Portail des mathématiques
Catégorie : Théorie des catégories
Wikimedia Foundation. 2010.