Développement En Série De Engel
- Développement En Série De Engel
-
Développement en série d'Engel
Construction du développement
Soit ![x_0 \in ]0,1]](/pictures/frwiki/49/1b251d6340799ccb99093ed8f3f16f14.png) . On construit le développement de ce nombre de la manière suivante :
. On construit le développement de ce nombre de la manière suivante :
![\left\{\begin{matrix} { a_0 = \left[\frac{1}{x_0}\right] + 1} \\ { x_1 = a_0x_0 - 1 } \end{matrix} \right.](/pictures/frwiki/53/5f6e1ae3bb8448c678a68d8d90e98b7a.png)
![\left\{\begin{matrix} { a_1 = \left[\frac{1}{x_1}\right] + 1} \\ { x_2 = a_1x_1 - 1 } \end{matrix} \right.\qquad
... \qquad
\left\{\begin{matrix} { a_n = \left[\frac{1}{x_n}\right] + 1} \\ { x_{n+1} = a_nx_n - 1 } \end{matrix} \right.](/pictures/frwiki/101/ee0d036e02ad7a1a11dbecae48daba3b.png) .
.
Dans ce cas, le nombre x0 s'écrit de manière unique sous la forme suivante (dite série de Engel) :
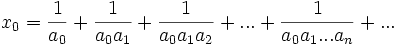
où la suite (an)n est une suite croissante d'entiers plus grands que 2.
Propriétés
Soit ![x_0 \in ]0,1]](/pictures/frwiki/49/1b251d6340799ccb99093ed8f3f16f14.png) . Alors x0 est rationnel si, et seulement si, la suite
. Alors x0 est rationnel si, et seulement si, la suite 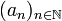 de son développement en série d'Engel est constante à partir d'un certain rang.
de son développement en série d'Engel est constante à partir d'un certain rang.
Exemples
Les nombres 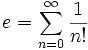 (qui donne immédiatement son développement : an = n) et
(qui donne immédiatement son développement : an = n) et 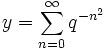 (avec
(avec 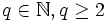 ) sont irrationnels car leurs développements en série d'Engel tendent vers l'infini.
) sont irrationnels car leurs développements en série d'Engel tendent vers l'infini.
 Portail des mathématiques
Portail des mathématiques
Bibliographie
- Théorie des nombres, Daniel Duverney
Catégories : Série | Fraction continue
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Développement En Série De Engel de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Developpement en serie de Engel — Développement en série d Engel Sommaire 1 Construction du développement 2 Propriétés 3 Exemples 4 Bibliographie // … Wikipédia en Français
Développement en série d'Engel — Sommaire 1 Construction du développement 2 Propriétés 3 Exemples 4 Bibliographie // … Wikipédia en Français
Développement en série de engel — Développement en série d Engel Sommaire 1 Construction du développement 2 Propriétés 3 Exemples 4 Bibliographie // … Wikipédia en Français
Développement en série de Engel — Le développement en série de Engel d un nombre réel positif y, moins connu que son développement en fraction continue mais étroitement lié, est son expression sous la forme (essentiellement unique) où les ak forment une suite croissante d entiers … Wikipédia en Français
Developpement en serie — Développement en série Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Un développement en série est l expression d une fonction sous forme d une série de fonctions élémentaires. Sur un domaine donné,… … Wikipédia en Français
Développement En Série — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Un développement en série est l expression d une fonction sous forme d une série de fonctions élémentaires. Sur un domaine donné, la fonction est égale à… … Wikipédia en Français
Développement en série — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Un développement en série est l expression d une fonction sous forme d une série de fonctions élémentaires. Sur un domaine donné, la fonction est égale à… … Wikipédia en Français
Friedrich Engel — Pour les articles homonymes, voir Friedrich Engels, Engel et Engels (homonymie). Friedrich Engel, né le 26 décembre 1861 à Lugau près de Chemnitz, mort le 29 septembre 1941 à Gießen, est un mathématicien allemand. Nommé à l université de Leipzig… … Wikipédia en Français
Powers (série télévisée) — Pour les articles homonymes, voir Powers. Powers Titre original Powers Genre Série fantastique science fiction Créateur(s) … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
![x_0 \in ]0,1]](/pictures/frwiki/49/1b251d6340799ccb99093ed8f3f16f14.png) . On construit le développement de ce nombre de la manière suivante :
. On construit le développement de ce nombre de la manière suivante :![\left\{\begin{matrix} { a_0 = \left[\frac{1}{x_0}\right] + 1} \\ { x_1 = a_0x_0 - 1 } \end{matrix} \right.](/pictures/frwiki/53/5f6e1ae3bb8448c678a68d8d90e98b7a.png)
![\left\{\begin{matrix} { a_1 = \left[\frac{1}{x_1}\right] + 1} \\ { x_2 = a_1x_1 - 1 } \end{matrix} \right.\qquad
... \qquad
\left\{\begin{matrix} { a_n = \left[\frac{1}{x_n}\right] + 1} \\ { x_{n+1} = a_nx_n - 1 } \end{matrix} \right.](/pictures/frwiki/101/ee0d036e02ad7a1a11dbecae48daba3b.png) .
.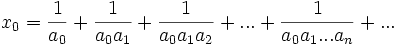
![x_0 \in ]0,1]](/pictures/frwiki/49/1b251d6340799ccb99093ed8f3f16f14.png) . Alors x0 est rationnel si, et seulement si, la suite
. Alors x0 est rationnel si, et seulement si, la suite 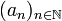 de son développement en série d'Engel est constante à partir d'un certain rang.
de son développement en série d'Engel est constante à partir d'un certain rang.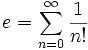 (qui donne immédiatement son développement : an = n) et
(qui donne immédiatement son développement : an = n) et 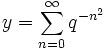 (avec
(avec 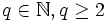 ) sont irrationnels car leurs développements en série d'Engel tendent vers l'infini.
) sont irrationnels car leurs développements en série d'Engel tendent vers l'infini.