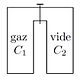
- Détente de Joule et Gay-Lussac
-
La détente de Joule Gay-Lussac est une détente adiabatique irréversible dans le vide. Pendant cette expérience, l'énergie interne du système reste constante : elle est donc isoénergétique.
On en déduit la première loi de Joule : « l'énergie interne d'un gaz parfait ne dépend que de sa température ».
Sommaire
Description de l'expérience
On considère deux récipients C1 de volume V1 et C2 de volume V2 aux parois adiabatiques et indéformables pouvant communiquer au moyen d'un robinet. Le premier C1 contient un gaz de pression P1 et de température T1, le deuxième récipient C2 est initialement vide.
On ouvre le robinet. Le gaz se répand alors dans C2 : cette diffusion est un processus spontané, non renversable et donc irréversible. L’état final du gaz est Pf,Vf,Tf .
Pour un gaz parfait, on constate expérimentalement que
.Interprétation
Le système considéré pour les deux calculs ci-dessous regroupe le récipient contenant initialement le gaz parfait à VA, PA et TA et celui contenant du vide, de volume VB.
Calcul de la variation d'énergie interne
Calculons la variation d'énergie interne ΔU du système considéré.
D'après le premier principe, on a : dU = δQ + δW
Or, la transformation est adiabatique donc δQ = 0. De plus, les parois sont indéformables donc dV = 0 (le volume ne varie pas), d'où :
.On en conclut que dU = 0, c'est-à-dire U = cte
Calcul de la variation d'entropie
Cherchons la variation d'entropie dans le cas de cette expérience, c'est-à-dire en considérant une transformation irréversible adiabatique sur un gaz parfait.
Comme la transformation est adiabatique (Sech = 0) irréversible (Scr > 0), on peut conclure que ΔS = Sech + Scr > 0
L'entropie étant une fonction d'état, elle ne dépend pas du chemin parcouru entre A et B mais seulement de l'entropie aux points A et B. Pour calculer la variation d'entropie ΔS, nous allons donc considérer la transformation réversible associée, qui passe par le même état initial (VA,TA) et le même état final (VB,TB = TA).
On obtient donc :
Or, d'après le premier principe :
(car la transformation est isoénergétique et réversible)D'où :
(loi des gaz parfaits)On intègre et on obtient finalement :
Voir aussi
Wikimedia Foundation. 2010.
