Dérivable par morceaux

Dérivable par morceaux

Régularité par morceaux

Certaines propriétés d'analyse sont énoncées avec des fonctions vérifiant des hypothèses telles que continu par morceaux, de classe 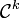\mathcal C^k par morceaux, etc.

Régularité par morceaux sur un segment

Une fonction f est continue par morceaux sur le segment [a,b] quand il existe une subdivision 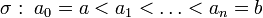\sigma :\; a_0=a<a_1<\dots <a_n=b telle que les restrictions de f à chaque intervalle ouvert ]ai,ai+1[ admettent un prolongement continu à l'intervalle fermé [ai,ai+1].

Concrètement une telle fonction f est continue sur ]ai,ai+1[ et admet une limite finie à droite et à gauche en chaque ai (lesquelles peuvent être distinctes et distinctes de la valeur de f au point ai lui-même).

On définit de même les fonctions de classe 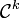\mathcal C^k par morceaux, linéaires par morceaux, etc.

On notera qu'une fonction de classe 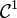\mathcal C^1 par morceaux, par exemple, n'est pas nécessairement continue en ai, mais qu'elle admet des limites et dérivées à droite et à gauche en ai.

Régularité par morceaux sur un intervalle

Une fonction est continue (ou autres propriétés) par morceaux sur l'intervalle I quand elle est continue (ou autre) par morceaux sur tout segment de I.

Domaines où l'on utilise la régularité par morceaux

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « R%C3%A9gularit%C3%A9 par morceaux ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Dérivable par morceaux de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Fonction affine par morceaux —  Ne pas confondre avec la notion d application linéaire par morceaux en géométrie. En mathématiques, une fonction affine par morceaux est une fonction définie sur une réunion d intervalles réels et dont la restriction à chacun de ces… …   Wikipédia en Français

  • Fonction Affine Par Morceaux — Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités …   Wikipédia en Français

  • Fonction continue dérivable nulle part — Fonction continue nulle part dérivable Sismogramme du Tremblement de terre de 1906 à San Francisco, bien que continue, cette courbe n est pas « arrondie ». En mathématiques, une fonction continue nulle part dérivable est une fonction… …   Wikipédia en Français

  • Fonction continue nulle part dérivable — Sismogramme du Tremblement de terre de 1906 à San Francisco, bien que continue, cette courbe n est pas « arrondie ». En mathématiques, une fonction continue nulle part dérivable est une fonction numérique qui est régulière du point de… …   Wikipédia en Français

  • FONCTIONS ANALYTIQUES - Fonctions d’une variable complexe — On se propose, dans ce premier article, d’exposer, avec des démonstrations quasiment complètes, les résultats les plus élémentaires de la théorie des fonctions analytiques d’une variable complexe; les deux derniers chapitres sont consacrés à… …   Encyclopédie Universelle

  • Coefficient de Fourier — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… …   Wikipédia en Français

  • Coefficients de Fourier — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… …   Wikipédia en Français

  • Décomposition d'un signal non sinusoïdal en séries de Fourier — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… …   Wikipédia en Français

  • Définition et décomposition en série de Fourier d'un signal non sinusoidal — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… …   Wikipédia en Français

  • Définition et décomposition en série de Fourier d'un signal non sinusoïdal — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”