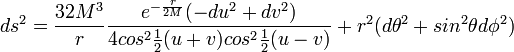Diagramme de penrose

Diagramme de Penrose d'un espace de Minkowski fini

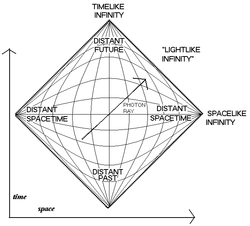
Les diagrammes de Penrose, inventés par le mathématicien britannique éponyme, sont une façon de représenter plusieurs métriques spatio-temporelles (solutions de l'équation d'Einstein) en supprimant systématiquement deux dimensions d'espace : la figure résultante est donc plane, représentable facilement dans le plan euclidien (c'est-à-dire une banale feuille de papier).

Diagramme de Penrose d'un espace de Schwarzschild.

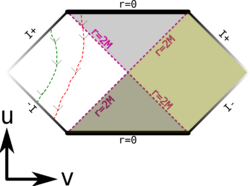
La figure à gauche montre la représentation d'un espace de Schwarzschild correspondant à un trou noir statique (pas de rotation). La coordonnée verticale nommée « u » est temporelle, alors que la coordonnée horizontale « v » est spatiale. Le diagramme de Penrose est conforme, c'est-à-dire que les géodésiques de genre nul (lignes de lumière) correspondent aux demi-première et deuxième bissectrices « hautes ».

Dans ce système de coordonnées, dérivé de celui de Kruskal, nous avons :

Le diagramme fait donc abstraction des deux coordonnées sphériques θ et φ. Les cônes de lumières délimités par les géodésiques nulles (ds² = 0) correspondent à du² = dv², donc {u = v} ou {u = -v}, c'est-à-dire les premières et deuxièmes bissectrices.

En partant de la gauche, deux droites (première et seconde bissectrices) divergent : la droite du bas, nommée I-, représente « l'infini du passé », là d'où proviennent tous les mobiles qui viennent de l'infiniment lointain ; la droite du haut, I+, correspond à « l'infini de l'avenir », et représente le lieu vers où se dirigent tous les mobiles qui s'éloignent à jamais du trou noir. Les deux droites horizontales et parallèles représentent la singularité (dans le passé et dans l'avenir), située en r = 0. Le diagramme est symétrique par rapport à la verticale. En pointillés, on a représenté l'horizon du trou noir, situé (en unités convenables) à r = 2M.

On peut donc distinguer quatre régions, suivant leur couleur :

1. Les zones de fond blanc correspondent à notre espace-temps, celles de fond marron à un espace-temps « miroir » ;
2. Les zones de fond clair sont dans l'espace « classique », les zones grisées à l'intérieur des horizons respectifs des singularités.

La singularité du passé (en bas de la figure) et l'espace « symétrique » situé à droite sont généralement considérés comme des artefacts mathématiques sans réalité physique. Ils sont de toute façon impossibles à atteindre. La singularité du passé se comporte comme un « trou blanc », à savoir une zone de répulsion gravitationnelle infinie : aucun mobile extérieur ne peut l'approcher en-deçà de son horizon, et tout ce qui se trouve crée à l'intérieur est expulsé — soit dans notre univers « normal » (à gauche), soit dans l'univers « miroir » (à droite).

Il est loisible d'identifier les « losanges » droite et gauche, ce qui revient à interpréter l'univers « miroir » comme une réplique mathématique de notre univers « normal ». Si l'on identifie en outre les singularités du haut et du bas, on arrive à un modèle physique où un trou noir éternel avale de la matière, rejetée dans un ailleurs spatio-temporel sous la forme de trou blanc.

Étude cinématique dans le diagramme de Penrose

En vert, on a représenté la trajectoire d'un mobile qui reste à distance du trou noir. Il émerge de I-, reste constamment dans son cône de lumière matérialisé par le « V » en pointillés (l'ensemble de ses vitesses permises, c'est à dire telles que |v| < c), puis atteint l'infini de l'avenir.

En rouge, on a représenté la trajectoire d'un mobile qui arrive de l'infini, se rapproche du trou noir puis dépasse l'horizon. On voit aisément qu'une fois au-delà de la droite r = 2M, en raison de la forme des cônes de lumière, quelle que soit la vitesse ultérieure du mobile, il ne peut que finir sur la singularité matérialisée par la droite du haut.

• Portail des mathématiques
• Portail de la cosmologie