Decouplage (automatique)

Decouplage (automatique): Découplage (automatique)

Le but du découplage est de transformer les fonctions de transfert ou les représentations d'états multivariables pour pouvoir commander chaque sortie indépendamment des autres.

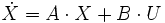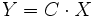Soit le système : $\dot X = A \cdot X + B \cdot U$ et $Y = C \cdot X$ avec dim x = m; dim u = p; dim y = p

d'où : 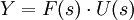$Y = F(s) \cdot U(s)$ avec $F (s) = C (s I - A) - 1 B$

F est appelé matrice de transfert carré.

Approche Fonction de transfert

En boucle fermé: $Y (s) = [I . p + F (s). C (s)] - 1 F (s) C (s) Y d (s)$ avec Yd la consigne

Le découplage consiste à diagonaliser le fonction de transfert en boucle fermé (FTBF).

$F T B F = [I . p + F (s). C (s)] - 1 F (s) C (s)$

Donc le correcteur C(s) doit vérifier: $[I p + F (s) C (s)] - 1 F (s) C (s) = Ω(s)$ avec $Ω(s)$ = matrice diagonale de $λ 1 (s)...λ n (s)$

On a donc : $C (s) = F (s) - 1 Ω(s)[I - Ω(s)] - 1$

Approche représentation d'état

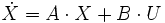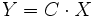
Soit le système : $\dot X = A \cdot X + B \cdot U$ et $Y = C \cdot X$

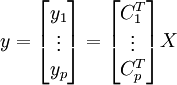
on a $y = \begin{bmatrix}y_1\\\vdots\\y_p\end{bmatrix} = \begin{bmatrix}C_1^T\\\vdots\\C_p^T\end{bmatrix}X$

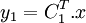
Pour $y 1$ : $y_1 = C_1^T.x$

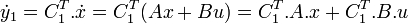
$\dot y_1 = C_1^T.\dot x = C_1^T(Ax+Bu) = C_1^T.A.x + C_1^T.B.u$

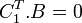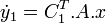
Si $C_1^T.B = 0$ alors $\dot y_1 = C_1^T.A.x$

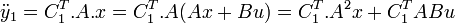
d'ou : $\ddot y_1 = C_1^T.A.x = C_1^T.A(Ax+Bu) = C_1^T.A^2x + C_1^TABu$

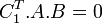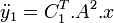
Si $C_1^T.A.B = 0$ alors $\ddot y_1 = C_1^T.A^2.x$

...

soit j le plus petit entier tel que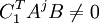 $C_1^TA^jB \not= 0$

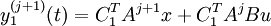
alors $y_1^{(j+1)}(t)=C_1^TA^{j+1}x+C_1^TA^jBu$

De meme pour les autres sorties :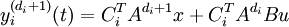 $y_i^{(d_i+1)}(t)=C_i^TA^{d_i+1}x+C_i^TA^{d_i}Bu$

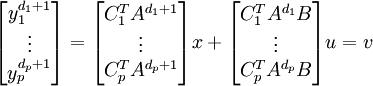
On obtient $\begin{bmatrix}y_1^{d_1+1}\\\vdots\\y_p^{d_p+1}\end{bmatrix} = \begin{bmatrix}C_1^TA^{d_1+1}\\\vdots\\C_p^TA^{d_p+1}\end{bmatrix}x + \begin{bmatrix}C_1^TA^{d_1}B\\\vdots\\C_p^TA^{d_p}B\end{bmatrix}u = v$

Y = Fx + Lu = v

on trouve donc $u = L - 1 [v - F x]$

Le système est découplale ssi L est inversible.

Le système découplé est donc transformé en sous-systèmes : 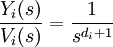$\frac{Y_i(s)}{V_i(s)}=\frac 1{s^{d_i+1}}$ On aboutit à des intégrateurs.

Portail des mathématiques

Ce document provient de « D%C3%A9couplage (automatique) ».

Catégorie : Automatique

Contenu soumis à la licence CC-BY-SA. Source : Article Decouplage (automatique) de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Découplage (Automatique) — Le but du découplage est de transformer les fonctions de transfert ou les représentations d états multivariables pour pouvoir commander chaque sortie indépendamment des autres. Soit le système : et avec dim x = m; dim u = p; dim y = p d… … Wikipédia en Français
Découplage (automatique) — En automatique, dans la perspective de règler un système dont l état est caractérisé par plusieurs variables, le but du découplage est de transformer la fonction de transfert ou la représentation d état afin de pouvoir commander chaque sortie… … Wikipédia en Français
AUTOMATIQUE — Automation, automatique, automatisation, automatismes, théorie des automates, cybernétique..., la variété même des vocables utilisés traduit la difficulté de définir précisément le contenu du substantif automatique . Nous choisirons ici d’appeler … Encyclopédie Universelle
Commande par découplage non-linéaire — La commande par découplage non linéaire est utilisée en automatique pour la commande des systèmes dynamiques non linéaires. Le principe de cette commande consiste à déterminer le correcteur de manière à compenser les effets non linéaires du… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Compatibilité électromagnétique — Chambre anéchoïque RF utilisée pour les essais CEM (émissions et immunités rayonnées) La compatibilité électromagnétique (CEM) est l aptitude d un appareil ou d un système électrique, ou électronique, à fonctionner dans son environnement… … Wikipédia en Français
Bruit radioélectrique — Compatibilité électromagnétique La compatibilité électromagnétique (CEM) est l aptitude d un appareil ou d un système électrique ou électronique à fonctionner dans son environnement électromagnétique de façon satisfaisante et sans produire lui… … Wikipédia en Français
Bruit électromagnétique — Compatibilité électromagnétique La compatibilité électromagnétique (CEM) est l aptitude d un appareil ou d un système électrique ou électronique à fonctionner dans son environnement électromagnétique de façon satisfaisante et sans produire lui… … Wikipédia en Français
Compatibilite electromagnetique — Compatibilité électromagnétique La compatibilité électromagnétique (CEM) est l aptitude d un appareil ou d un système électrique ou électronique à fonctionner dans son environnement électromagnétique de façon satisfaisante et sans produire lui… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Decouplage (automatique)

Découplage (automatique)

Approche Fonction de transfert

Approche représentation d'état

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Decouplage (automatique)

Découplage (automatique)

Approche Fonction de transfert

Approche représentation d'état

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link