Davis-Putnam
- Davis-Putnam
-
Algorithme de Davis-Putnam
En calcul propositionnel, l'algorithme de Davis-Putnam est une méthode de détermination de la satisfiabilité d'une formule en forme normale conjonctive, c'est-à-dire une conjonction de clauses (disjonctions de littéraux). Il a été développé par Martin Davis et Hilary Putnam.
Algorithme
- pour chaque variable dans la formule
- pour chaque clause C contenant la variable et chaque clause N contenant la négation de cette variable
- résoudre C et N et ajouter la solution à la formule
- retirer les clauses contenant la variable ou sa négation
Algorithme récursif
DP(T)
- Si T est vide alors retourner
Vrai
- Si T est la clause vide alors retourner
Faux
- Choisir une variable Xi dans T
- retourner
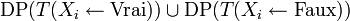
Voir aussi
 Portail de la logique
Portail de la logique Portail de l’informatique
Portail de l’informatique
Catégories : Algorithme | Logique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Davis-Putnam de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Davis–Putnam algorithm — The Davis–Putnam algorithm was developed by Martin Davis and Hilary Putnam for checking the validity of a first order logic formula using a resolution based decision procedure for propositional logic. Since the set of valid first order formulas… … Wikipedia
Davis-Putnam-Algorithmus — Das Davis Putnam Verfahren (nach Martin Davis und Hilary Putnam) entscheidet über die Unerfüllbarkeit einer aussagenlogischen Formel in Konjunktiver Normalform. Das Verfahren sollte nicht mit der Weiterentwicklung, dem DPLL (Davis Putnam Logemann … Deutsch Wikipedia
Davis-Putnam-Verfahren — Das Davis Putnam Verfahren (nach Martin Davis und Hilary Putnam) entscheidet über die Unerfüllbarkeit einer aussagenlogischen Formel in Konjunktiver Normalform. Das Verfahren sollte nicht mit der Weiterentwicklung, dem DPLL (Davis Putnam Logemann … Deutsch Wikipedia
Algoritmo de Davis-Putnam — El algoritmo de Davis Putnam fue desarrollado por Martin Davis y Hilary Putnam para comprobar la satisfacibilidad de las fórmulas de la lógica proposicional en forma normal conjuntiva, es decir, en conjuntos de cláusulas. Esto es una forma de… … Wikipedia Español
Algorithme De Davis-Putnam — En calcul propositionnel, l algorithme de Davis Putnam est une méthode de détermination de la satisfiabilité d une formule en forme normale conjonctive, c est à dire une conjonction de clauses (disjonctions de littéraux). Il a été développé par… … Wikipédia en Français
Algorithme de davis-putnam — En calcul propositionnel, l algorithme de Davis Putnam est une méthode de détermination de la satisfiabilité d une formule en forme normale conjonctive, c est à dire une conjonction de clauses (disjonctions de littéraux). Il a été développé par… … Wikipédia en Français
Méthode de Davis-Putnam — Algorithme de Davis Putnam En calcul propositionnel, l algorithme de Davis Putnam est une méthode de détermination de la satisfiabilité d une formule en forme normale conjonctive, c est à dire une conjonction de clauses (disjonctions de… … Wikipédia en Français
Algorithme de Davis-Putnam — En calcul propositionnel, l algorithme de Davis Putnam est une méthode de détermination de la satisfiabilité d une formule en forme normale conjonctive, c est à dire une conjonction de clauses (disjonctions de littéraux). Il a été développé par… … Wikipédia en Français
Davis — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Cet article possède des paronymes, voir : Davies et Davy. Le nom Davis peut désigner des personnes (nom de famill … Wikipédia en Français
Putnam County (Georgia) — Putnam County Courthouse im Eatonton Historic District, gelistet im NRHP Nr. 75000605[1] Verwaltung … Deutsch Wikipedia