Accélération séculaire

Effet Shklovski

En astronomie, l'effet Shklovski est le nom donné à la variation de la période apparente d'un pulsar du simple fait de son déplacement dans l'espace, à l'image d'un effet Doppler-Fizeau qui voit la fréquence du son émis par une source varier quand celle-ci passe devant l'observateur. En pratique, la variation de la période du signal émis par un pulsar peut être interprétée comme étant due à une variation de vitesse de celui-ci, c'est-à-dire une accélération. Pour cette raison, le terme d'accélération séculaire est parfois utilisé en lieu et place d'effet Shklovsky, donnée en l'honneur de l'astronome russe I. S. Shklovsky qui l'a mis en évidence en 1970^[1].

Calcul de l'effet Shklovski

L'effet Shklovski n'est rien d'autre que le calcul classique de l'effet Doppler en tenant compte du déplacement de la source d'un signal périodique. Il prédit que l'on mesure une variation apparente 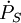$\dot P_S$ de la période $P$ du signal émis par un pulsar donnée par

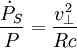$\frac{\dot P_S}{P} = \frac{v_\perp^2}{R c}$ ,

où R est la distance du pulsar, c la vitesse de la lumière et 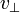$v_\perp$ la norme de la composante de la vitesse perpendiculaire à la direction dans laquelle se trouve le pulsar.

Démonstration

Soit $P 0$ la période du signal du pulsar. La période apparente $P$ mesurée par un observateur situé à l'origine du système de coordonnées s'écrit :

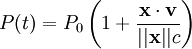$P (t) = P_0 \left(1 + \frac{{\mathbf{x}} \cdot {\mathbf{v}}}{||{\mathbf{x}}|| c} \right)$ .

La dérivée de cette quantité, notée par un point se calcule immédiatement en

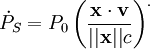$\dot P_S = P_0 \left(\frac{{\mathbf{x}} \cdot {\mathbf{v}}}{||{\mathbf{x}}|| c} \right)^.$ ,

ce qui donne, en développant

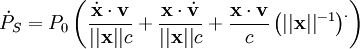$\dot P_S = P_0 \left(\frac{\dot {\mathbf{x}} \cdot {\mathbf{v}}}{||{\mathbf{x}}|| c} + \frac{{\mathbf{x}} \cdot \dot {\mathbf{v}}}{||{\mathbf{x}}|| c} + \frac{{\mathbf{x}} \cdot {\mathbf{v}}}{c} \left(||{\mathbf{x}}||^{-1}\right)^.\right)$ ,

c'est-à-dire

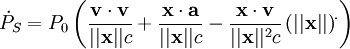$\dot P_S = P_0 \left(\frac{{\mathbf{v}} \cdot {\mathbf{v}}}{||{\mathbf{x}}|| c} + \frac{{\mathbf{x}} \cdot {\mathbf{a}}}{||{\mathbf{x}}|| c} - \frac{{\mathbf{x}} \cdot {\mathbf{v}}}{||{\mathbf{x}}||^2 c} \left(||{\mathbf{x}}||\right)^.\right)$ ,

a étant l'accélération du pulsar. En notant avec l'indice 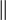$\parallel$ la composante des vecteur le long de la ligne de visée et R la distance 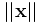$||{\mathbf{x}}||$ , il vient

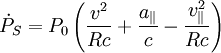$\dot P_S = P_0 \left(\frac{v^2}{R c} + \frac{a_\parallel}{c} - \frac{v_\parallel^2}{R c} \right)$ ,

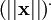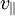puisque la quantité $\left(||{\mathbf{x}}||\right)^.$ représente la variation de la distance du pulsar, c'est-à-dire la composante de sa vitesse radiale $v_\parallel$ .

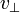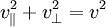Dans le cas où le pulsar est en mouvement rectiligne uniforme, son accélération est nulle, et il reste, en notant $v_\perp$ le module de la composante transverse de la vitesse ( $v_\parallel^2 + v_\perp^2 = v^2$ ),

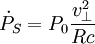$\dot P_S = P_0 \frac{v_\perp^2}{R c}$ .

En supposant que la vitesse du pulsar est petite devant la vitesse de la lumière, l'on peut approximer la période $P (t)$ par $P 0$ , d'où finalement

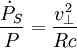$\frac{\dot P_S}{P} = \frac{v_\perp^2}{R c}$ .

Dans le cas où le pulsar subit une accélération, alors il faut tenir compte du terme en a dans la dérivation. L'on sait que la partie radiale de l'accélération, 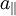$a_\parallel$ , est donnée par (voir Coordonnées polaires en analyse vectorielle)

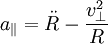$a_\parallel = \ddot R - \frac{v_\perp^2}{R}$ ,

d'où on déduit la formule générale

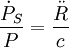$\frac{\dot P_S}{P} = \frac{\ddot R}{c}$ .

Même dans le cas où l'accélération est nulle, cette formule reste valable. En effet, le fait que la vitesse du pulsar soit constante ne signifie pas que sa distance à l'observateur croisse linéairement avec le temps. Si l'on note $R m$ la distance minimale d'approche du pulsar que l'on suppose animé d'une vitesse constante v, alors sa distance R à l'observateur évolue selon

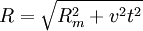$R = \sqrt{R_m^2 + v^2 t^2}$ .

Cette fonction tend vers une fonction linéaire du temps à grand t Dans ce cas là, la trajectoire du pulsar est quasiment radiale, et on n'observe quasiment pas de variation de période, mais la quantité 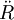$\ddot R$ est toujours non nulle (et toujours positive).

Ordre de grandeur et mise en évidence

Un pulsar ordinaire est animé d'une vitesse typique de 1 000 km/s et situé à une distance typique de l'ordre de quelques kiloparsecs, l'application numérique donne

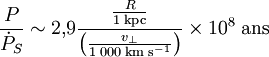$\frac{P}{\dot P_S} \sim 2,\!9 \frac{\frac{R}{1\;{\mathrm{kpc}}}}{\left(\frac{v_\perp}{1\;000\;{\mathrm{km}}\;{\mathrm{s}}^{-1}}\right)} \times 10^8\;{\mathrm{ans}}$ .

En pratique, un pulsar voit sa rotation ralentir au cours du temps (voir Ralentissement des pulsars), du fait qu'il dissipe de l'énergie électromagnétique du fait de sa rotation, et que cette perte d'énergie est compensée par une perte d'énergie cinétique de rotation. La période réelle d'un pulsar décroît donc au cours du temps d'une quantité 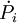$\dot P_i$ . Cette quantité 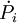$\dot P_i$ permet de calculer l'âge caractéristique $t c$ d'un pulsar, qui correspond sous certaines hypothèses (voir Âge caractéristique), à l'âge réel du pulsar. L'âge caractéristique est donné par

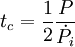$t_c = \frac{1}{2} \frac{P}{\dot P_i}$ .

En pratique, on observe la combinaison du ralentissement apparent 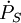$\dot P_S$ dû à l'effet Schklovski et du ralentissement intrinsèque 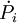$\dot P_i$ du pulsar, qu'il n'est pas possible de distinguer par la seule observation du ralentissement (réel et apparent) du pulsar. Ainsi, l'âge caractéristique mesuré $t m$ est-il

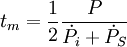$t_m = \frac{1}{2} \frac{P}{\dot P_i + \dot P_S}$ ,

que l'on peut réécrire en

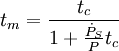$t_m = \frac{t_c}{1 + \frac{\dot P_S}{P} t_c}$ .

En pratique, l'effet Schkolvski bruite la mesure de l'âge caractéristique, mais n'est gênante que dans les cas où l'âge caractéristique est de l'ordre de ou plus grand que l'ordre de grandeur donné ci-dessus. L'effet n'est donc gênant que pour les pulsars suffisamment âgés, ce qui concerne essentiellement les pulsars millisecondes.

L'effet Shklovski peut toutefois être distingué du ralentissement intrinsèque si l'on parvient à mesurer la vitesse transverse du pulsar et sa distance. La distance peut être mesurée soit directement par parallaxe ou parallaxe chronométrique, soit indirectement par la mesure de dispersion ou l'absorption HI. La vitesse se déduit alors par la mesure du mouvement propre du pulsar, c'est-à-dire son déplacement sur la sphère céleste. Dans les deux cas, il est préférable que le pulsar soit proche, de façon à ce que les effets de parallaxe et le mouvement propre soient importants. Pour le pulsar PSR B1133+16, il a ainsi pu être mis en évidence que l'effet Shklovski était responsable de 5 % environ du ralentissement observé. Il est possible que pour des pulsars millisecondes, il soit la contribution dominante de celui-ci.

Une autre situation où l'effet Shklovski est plus facile à mettre en évidence est celui où la période du phénomène observé n'a pas de raison de varier au cours du temps. C'est par exemple le cas pour la période orbitale d'un système binaire. Celle-ci peut être amenée à décroître du fait de l'émission de rayonnement gravitationnel (comme pour le pulsar binaire PSR B1913+16), mais une augmentation de celle-ci peut révéler l'effet Shklovski à l'œuvre. PSR J0437-4715, un pulsar binaire, est le premier dont les paramètres ont pu être mesurés avec suffisamment de précision pour qu'il eût pu être établi que le ralentissement de sa période orbitale était entièrement due à l'effet Shklovski^[2].

Accélération des pulsars

La formule exacte de l'effet Shklovski est en réalité (voir démonstration ci-dessus)

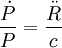$\frac{\dot P}{P} = \frac{\ddot R}{c}$ ,

où intervient la dérivée seconde de la distance R au pulsar. Quand le pulsar ne se déplace pas le long de la ligne de visée, un mouvement rectiligne uniforme donne lieu à une dérivée seconde de la distance. Cependant, il est aussi possible que cette dérivée seconde soit non nulle si le pulsar accélère. Celle-ci peut du reste être explicitement être mise en évidence si le pulsar accélère vers l'observateur, auquel cas la quantité 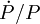$\dot P / P$ est négative, et ne peut correspondre à un ralentissement intrinsèque. Ceci se produit pour des pulsars situés dans des puits de potentiel marqués comme des amas globulaires, quand le pulsar est approximativement situé dans l'alignement de l'observateur et du centre du puits, et derrière celui-ci. Ces conditions sont réunies pour les deux pulsars PSR B2127+11A et PSR B2127+11D situés dans l'amas M15 qui présentent chacun un 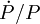$\dot P / P$ de l'ordre de -2,0×10^-16 s^-1.

Voir aussi

Référence

(en) Andrew G. Lyne & Francis Graham Smith, Pulsar astronomy, Cambridge University Press, 2^e édition, 264 pages (1998) ISBN 0-521-59413-8, page 55.

Note

↑ I. S. Shklovski, Possible causes of secular increase in pulsar period, Soviet Astronomy, 13, 562 (1970) Voir en ligne.
↑ Voir (en) Jon F. Bell et al., The proper motion and wind nebula of the nearby millisecond pulsar J0437-4715, Astrophysical Journal, 440, L81-L83 (1995) Voir en ligne ; (en) S. M. Kopeikin, Proper motion of binary pulsars as a source of secular variation of orbital parameters, Astrophysical Journal, 467, L93-L95 (1996) Voir en ligne.

Portail de l’astronomie

Ce document provient de « Effet Shklovski ».

Catégorie : Pulsar

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Accélération séculaire de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Accélération de la gravité — Pesanteur Ne doit pas être confondu avec apesanteur. Schéma montrant la vitesse d un objet en fonction du temps lorsqu i … Wikipédia en Français
Accélération de la pesanteur — Pesanteur Ne doit pas être confondu avec apesanteur. Schéma montrant la vitesse d un objet en fonction du temps lorsqu i … Wikipédia en Français
Liste De Pulsars Notables — Cette page recense divers pulsars présentant un intérêt notable en astrophysique. Désignation Notes P (s) (s·s 1) PSR B0042 73 Premier pulsar détecté dans le Petit Nuage de Magellan Pulsar binaire 0,926275835356(15) 4,486(1)×10 15 PS … Wikipédia en Français
Liste de pulsars notables — Cette page recense divers pulsars présentant un intérêt notable en astrophysique. Désignation Notes P (s) (s·s 1) PSR B0042 73 Premier pulsar détecté dans le Petit Nuage de Magellan Pulsar binaire 0,926275835356(15) 4,486(1)×10 15 PSR J0100 7211 … Wikipédia en Français
Pierre-Simon Laplace — Laplace redirects here. For the city in Louisiana, see LaPlace, Louisiana. For the joint NASA ESA space mission, see Europa Jupiter System Mission. Pierre Simon, marquis de Laplace Pierre Simon Laplace (1749–1827). Posthumous portrait … Wikipedia
Effet Shklovski — En astronomie, l effet Shklovski est le nom donné à la variation de la période apparente d un pulsar du simple fait de son déplacement dans l espace, à l image d un effet Doppler Fizeau qui voit la fréquence du son émis par une source varier… … Wikipédia en Français
Effet Shklovsky — Effet Shklovski En astronomie, l effet Shklovski est le nom donné à la variation de la période apparente d un pulsar du simple fait de son déplacement dans l espace, à l image d un effet Doppler Fizeau qui voit la fréquence du son émis par une… … Wikipédia en Français
Ernest W. Brown — Ernest William Brown Ernest William Brown (29 novembre 1866 22 juillet 1938) est un mathématicien et astronome américain d origine britannique. Brown passe la plus grande partie de sa vie à étudier l orbite lunaire et à compiler des tables… … Wikipédia en Français
Ernest William Brown — (29 novembre 1866 22 juillet 1938) est un mathématicien et astronome américain d origine britannique. Il a passé la plus grande partie de sa vie à étudier l orbite lunaire et à compiler des tables lunaires très précises. Il a aussi étudié le… … Wikipédia en Français
Пюизё, Виктор-Александр — (Puiseux) французский математик и астроном (1820 1883). По окончании курса в нормальной школе был профессором математики в безансонском факультете, а затем последовательно распорядителем лекций нормальной школы, адъюнкт астрономом в парижской… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Dictionnaires et Encyclopédies sur 'Academic'

Accélération séculaire

Effet Shklovski

Sommaire

Calcul de l'effet Shklovski

Ordre de grandeur et mise en évidence

Accélération des pulsars

Voir aussi

Référence

Note

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Accélération séculaire

Effet Shklovski

Sommaire

Calcul de l'effet Shklovski

Ordre de grandeur et mise en évidence

Accélération des pulsars

Voir aussi

Référence

Note

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link