Cube de hilbert
- Cube de hilbert
-
Cube de Hilbert
En topologie, on appelle cube de Hilbert l'espace produit ![K = \left[0,1\right]^{\mathbb N}](/pictures/frwiki/50/2018949361ab4610d25ec3e9d9c7f7fc.png) muni de la topologie produit. D'après le théorème de Tychonoff, c'est un espace compact.
muni de la topologie produit. D'après le théorème de Tychonoff, c'est un espace compact.
Il est homéomorphe à ![\left[0,1\right] \times \left[0,\frac12\right] \times \left[0,\frac13\right] \times
\cdots](/pictures/frwiki/53/5c1978a7f54c943be56379ebc5c5e39f.png) , ou à l'espace des suites
, ou à l'espace des suites 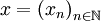 , telles que
, telles que 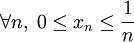 , muni de la distance :
, muni de la distance :
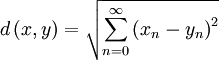 .
.
Il s'agit donc d'un espace métrisable.
Il est à base dénombrable (en fait, pour un espace compact, être métrisable ou être à base dénombrable sont des propriétés équivalentes), et possède la propriété universelle suivante :
- « Tout espace métrisable à base dénombrable est homéomorphe à un sous-espace de K. »
Cela fournit en particulier un moyen commode pour compactifier les espaces métrisables à base dénombrable, et aussi un critère pour les classifier selon leur complexité ; par exemple un espace est polonais si et seulement s'il est homéomorphe à l'intersection d'une suite d'ouverts de K. On en déduit aussi que tout espace mesurable dénombrablement engendré et séparé est isomorphe à une partie de K munie de la tribu induite par la tribu borélienne de K.
 Portail des mathématiques
Portail des mathématiques
Catégorie : Analyse fonctionnelle
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Cube de hilbert de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Cube De Hilbert — En topologie, on appelle cube de Hilbert l espace produit muni de la topologie produit. D après le théorème de Tychonoff, c est un espace compact. Il est homéomorphe à , ou à l espace des suites , telles que … Wikipédia en Français
Cube de Hilbert — En topologie, on appelle cube de Hilbert l espace produit muni de la topologie produit. D après le théorème de Tychonoff, c est un espace compact. Il est homéomorphe à , ou à l espace des suites , telles que … Wikipédia en Français
Hilbert — David Hilbert David Hilbert David Hilbert en 1912 Naissance 23 janvier 1862 Königsberg (Prusse Orientale) … Wikipédia en Français
HILBERT (PROBLÈMES DE) — «Qui ne se réjouirait de pouvoir soulever le voile qui cache le futur, de jeter un regard sur le développement des mathématiques, ses progrès ultérieurs, les secrets des découvertes des siècles à venir?...» Prévoir le futur des mathématiques: qui … Encyclopédie Universelle
Hilbert cube — In mathematics, the Hilbert cube, named after David Hilbert, is a topological space that provides an instructive example of some ideas in topology.DefinitionThe Hilbert cube is best defined as the topological product of the intervals [0,1/n]… … Wikipedia
Hilbert's third problem — The third on Hilbert s list of mathematical problems, presented in 1900, is the easiest one. The problem is related to the following question: given any two polyhedra of equal volume, is it always possible to cut the first into finitely many… … Wikipedia
David Hilbert — en 1912 Naissance 23 janvier 1862 Königsberg (Prusse Orientale) Décès 14 février 1943 … Wikipédia en Français
David Hilbert — Hilbert redirects here. For other uses, see Hilbert (disambiguation). David Hilbert David Hilbert (1912) Born … Wikipedia
Problèmes de Hilbert — Lors du deuxième congrès international des mathématiciens tenu à Paris en 1900, David Hilbert présenta une liste de problèmes qui tenaient jusqu alors les mathématiciens en échec. Ces problèmes devaient, selon Hilbert, marquer le cours des… … Wikipédia en Français
Problemes de Hilbert — Problèmes de Hilbert Lors du deuxième congrès international de mathématiques tenu à Paris en 1900, David Hilbert présenta une liste de problèmes qui tenaient jusqu alors les mathématiciens en échec. Ces problèmes devaient, selon Hilbert, marquer… … Wikipédia en Français
![K = \left[0,1\right]^{\mathbb N}](/pictures/frwiki/50/2018949361ab4610d25ec3e9d9c7f7fc.png) muni de la topologie produit. D'après le théorème de Tychonoff, c'est un espace compact.
muni de la topologie produit. D'après le théorème de Tychonoff, c'est un espace compact.![\left[0,1\right] \times \left[0,\frac12\right] \times \left[0,\frac13\right] \times
\cdots](/pictures/frwiki/53/5c1978a7f54c943be56379ebc5c5e39f.png) , ou à l'espace des suites
, ou à l'espace des suites 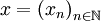 , telles que
, telles que 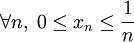 , muni de la distance :
, muni de la distance :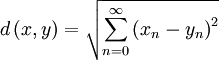 .
.