Crénelage

Pour les articles homonymes, voir repliement.

Le crénelage (ou crènelage) ou repli de spectre (Aliasing en anglais) est un phénomène qui peut se produire lors du traitement numérique d'un signal, lorsque des fréquences qui ne sont pas représentées dans le signal original sont introduites par erreur dans le signal, par conséquence de son échantillonnage (voir le Théorème d'échantillonnage de Nyquist-Shannon). Mais le crénelage est également un phénomène se produisant lors de la réduction (avec pertes) d'un signal d'un espace constitué de nombres réels vers un espace constitué de nombres entiers.

Notamment dans le domaine du jeu vidéo et de l'électronique on utilise aussi assez souvent l'anglicisme aliasing.

Espaces numériques

Tout signal, qu'importe le nombre de ses dimensions, appartient à (au moins) un ensemble numérique. Un crénelage apparaît lors du passage d'un ensemble appartenant aux nombres réels à un ensemble appartenant aux nombres entiers .

Le signal, constituant une suite de nombres, doit alors être « réduit » au mieux. Pour passer d'un nombre réel à un nombre entier, généralement, on arrondit le nombre réel au nombre entier le plus proche. Mais on peut également l'arrondir soit au nombre entier inférieur, soit au nombre entier supérieur selon les contraintes techniques. C'est ainsi qu'un crénelage irréversible du signal apparaît.

5,6   donnera  6   s'il est arrondi à l'entier le plus proche
5,6   donnera  5   s'il est arrondi à l'entier inférieur le plus proche
5,3   donnera  6   s'il est arrondi à l'entier supérieur le plus proche

Une autre méthode de conversion consiste à enlever la partie décimale des nombres réels . Ainsi, les résultats sont différents lorsqu'on utilise des nombres relatifs (nombres signés, c'est-à-dire, pouvant être positifs ou négatifs).

Le facteur technologique

Le phénomène du crénelage est étroitement lié au facteur technologique. Ainsi, en informatique, on utilisera, tant matériellement que logiciellement, des matrices afin de stocker l'information d'un signal. Cependant, ce facteur ne constitue qu'une contrainte dont on peut s'extraire selon la manière dont on interprète les informations stockées. Ainsi, on peut parfaitement stocker des valeurs numériques appartenant au domaine des nombres réels. Mais la technologie a ses limites. Ainsi, la précision des nombres réels (c'est-à-dire, le nombre de décimales) aura ses propres limites d'un système technologique à un autre et sera un facteur prépondérant à l'effet de crénelage.

Imagerie numérique

Exemple de crénelage sur la lettre A en Times New Roman. A gauche l'image crénelée, à droite l'image anticrénelée.

L'imagerie numérique a cette particularité d'être souvent appliquée à des espaces matriciels. Dans ce type d'environnement, les règles de la géométrie euclidienne sont profondément bouleversées. Par exemple, le théorème de Pythagore ne s'y appliquera pas.

Il est cependant nécessaire de bien distinguer les deux branches fondamentales de l'imagerie numérique. Ainsi, l'imagerie numérique dite « vectorielle », ne souffre de ce phénomène de crénelage que par les limitations techniques dans son utilisation, dues essentiellement à la précision des nombres réels stockés et/ou reproduits.

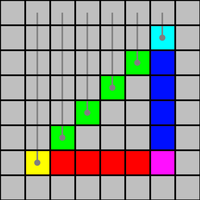
En imagerie matricielle (parfois dite « pixelique » du fait de l'utilisation de pixels), le phénomène de crénelage peut se produire de différentes manières. L'exemple le plus récurrent est sans doute le tracé d'un segment. Classiquement, on utilisera la fonction affine (f(x) = ax + b) pour le tracé d'un segment. Le crénelage se produira alors lorsque la largeur et la hauteur différeront l'une de l'autre. Pour pallier ce problème (voir l'article anticrénelage), on fera appel à l'algorithme de tracé de segment de Xiaolin Wu. On parlera alors de « Wu pixeling ».

Cette technique consiste essentiellement à transformer les pixels matriciels en « pixels vectoriels » avant de tracer le segment comme en géométrie traditionnelle (i.e., en espace euclidien). La notion de « pixel vectoriel » peut paraître paradoxale et c'est pour cela que certains lui préfèrent la notion de « point graphique vectoriel ». L'idée sous sous-jacente est de considérer le centre de chaque pixel comme étant la correspondance entre nombres entiers et nombres réels. Ainsi, la taille de chaque pixel vectoriel reste bien égale à 1 pixel (taille variable, d'où un certain intérêt) mais chaque pixel ira de > -0,5 à +0,5 relativement à son unité en nombres réels. Ensuite, on calculera chaque surface que le pixel vectoriel recouvre sur ses pixels matriciels adjacents. Après, on devra faire une synthèse additive de la couleurs initiale de chaque pixels matriciel adjacent avec la couleur du pixel vectoriel selon la surface que ce dernier recouvre. Il est à noter que ceci constitue la base du procédé de rendu 2D des boxels et autres voxels.

Le crénelage peut également arriver lorsque l'on redimensionne une image vers une résolution différente à la résolution de numérisation. Si on la réduit, il s'ensuit cet effet de pixellisation, plus ou moins marqué, sur les bordures d'éléments visuels, ou entre éléments visuels adjacents. Ceci est dû à la manière dont la perte d'informations s'opère. Ce ré-échantillonnage peut s'opérer de bien des manières. Une approche naïve consistera à ne conserver que les pixels existants selon l'approximation de leur position relative. Le résulta sera épouvantable. Une des solutions (voir plus bas) viables réside dans la vectorisation de l'image d'origine afin de la tracer réduite avec des « Wu-pixels ». Cela revient plus ou moins à faire une moyenne chromatique de chaque zone enlevée. Dans le cas d'un agrandissement, le phénomène apparaîtra si l'on redessine les pixels sous la forme de carrés proportionnels au lieu de les considérer tel des points de couleurs qu'il faut lier par des dégradés.

Imagerie 3D

Ce domaine est complexe et les méthodes de rendu sont extrêmement variées selon les utilisations et ce phénomène peut apparaître pour diverses raisons selon les procédés de rendu employés. Par conséquent, les solutions sont très variées tant sur le plan conceptuel que sur les plans mathématique, algorithmique et technique.

On peut néanmoins classer ces méthodes selon :

• qu'elles soient vectorielles (la grande majorité des cas; citons par exemple le ray-tracing) ou matricielles (tel que l'approche par voxels/boxels)
• qu'elles soient destinées à un rendu en temps réel (le cas des jeux vidéo) ou non (cas des logiciels d'animation 3D)
• qu'elles utilisent les fonctions matérielles ou logicielles,

Néanmoins, beaucoup de méthodes mélangent tous ces procédés pour arriver à leurs fins.

Le domaine le plus inventif en matière de solutions reste celui des jeux vidéo en 3D qui utilisent autant des procédés matériels que logiciels.

On notera cependant que les techniques d'anti-crénelage sont généralement orientées vers une approche du traitement global de l'image.

Cinéma et vidéo

L'exemple le plus classique de crénelage est probablement celui de la roue de charrette dans un western : les rayons sont vus en rotation lente et souvent (statistiquement, une fois sur deux) inverse au déplacement réel de la roue. Interpoler deux images successives afin de les afficher à une fréquence bien plus élevée (lors d'une conversion à un format numérique) ne corrige rien : on ne peut pas restituer l'information perdue par l'échantillonnage initial à 24 Hz. En termes techniques, on observe donc le « repli » (ou repliement) d'une fréquence supérieure à la fréquence de Nyquist vers une fréquence inférieure à celle-ci. Ce terme se comprend si on imagine que le spectre du signal (de zéro Hz à l'infini) est « replié » en accordéon entre 0 et la fréquence de Nyquist. La figure ci-dessous montre comment une fréquence de f = 0,9 est repliée vers f = 0,1 si f_Nyquist = 1 / (2T) = 0,5.

Si dans d'autres domaines le filtrage préalable du signal (pour supprimer toute composante supérieure à la fréquence de Nyquist) évite l'apparition de ces fréquences « fantômes » (alias), ce filtrage n'est pas toujours possible voire même désirable en cinéma/vidéo. La roue de charrette apparaîtrait fixe à partir d'une certaine vitesse, ce qui serait visuellement encore pire...

Photo

Lors de la photographie d'une scène avec un capteur numérique, les fréquences spatiales présentes dans l'image et supérieure à la fréquence de Nyquist peuvent être repliées vers une fréquence inférieure. Ceci se traduit alors par des effets de « grille » ou de moiré coloré (sur les capteurs à matrice de Bayer, les plus courants). Pour éviter ces artefacts, les fréquences supérieures à la fréquence de Nyquist sont généralement supprimées du signal par un filtre passe-bas placé devant le capteur.

Domaine du son

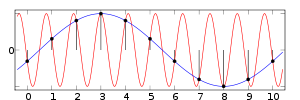Ce graphique démontre le crénelage d'un signal sinusoïdal de fréquence f=0.9, confondu avec un signal de fréquence f=0.1 lors d'un échantillonnage de période T=1.0.

Le crénelage sonore consiste également en un « repli » d'une fréquence supérieure à la fréquence de Nyquist vers une fréquence inférieure à celle-ci. Ceci est particulièrement gênant puisque ce phénomène peut transformer une harmonique d'un son en une fréquence anharmonique^[1], déplaisante à l'oreille. Le crénelage est souvent une conséquence des opérations de rééchantillonnage (l'équivalent sonore du redimensionnement d'image, utilisé dans les échantillonneurs pour varier la hauteur d'un son) ou de distorsion (utilisée notamment pour simuler des amplificateurs à lampes).

Solutions

Dans bien des cas il n'est malheureusement pas possible mathématiquement d'éliminer rigoureusement le crénelage, mais il est toutefois possible de le réduire à des niveaux infimes. Une technique courante est de suréchantillonner le signal à une fréquence d'échantillonnage nettement supérieure à la fréquence voulue, appliquer les traitements voulus (par exemple redimensionnement d'image, rééchantillonnage ou distorsion de son), puis de lui appliquer un filtre passe-bas pour éliminer toute fréquence supérieure à la fréquence de Nyquist. On peut alors redescendre en toute sécurité à la fréquence d'échantillonnage voulue, puisqu'aucune fréquence supérieure à la fréquence de Nyquist n'est présente. Cette méthode nécessite une puissance de calcul très importante, elle n'est donc pas applicable à toutes les situations : c'est ainsi qu'à l'heure actuelle, nombre de jeux vidéo préfèrent encore consacrer toute la puissance du processeur graphique à l'affichage de détails supplémentaires plutôt qu'à la réduction du crénelage.

Notes et références

Annexes

Articles connexes

• Traitement numérique du signal

• Portail des télécommunications
• Portail de l’imagerie numérique