Crémona

L'épure de Cremona — du nom de son inventeur, Luigi Cremona, mais on trouve fréquemment les orthographes avec un accent aigu et éventuellement une minuscule initiale (Crémona, crémona) — est une méthode de statique graphique utilisée pour le calcul des efforts dans un treillis (système triangulé, assemblage de poutres).

Description

Exemple d'épure de Cremona (à droite) pour une structure simple (à gauche).

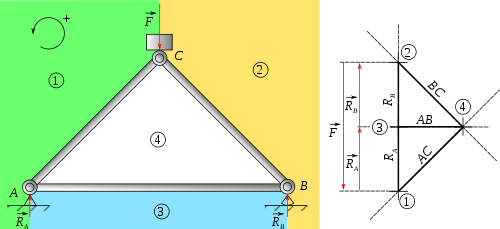
La structure est divisée en régions, qui sont délimitées par des poutres ou les demi-droites portant les forces extérieures à la structure. Dans le diagramme — épure de Cremona, ou Cremona tout court —, les régions sont représentées par un point. Sur cette épure, les points représentant deux régions contiguës sont reliés par un segment ayant la direction de la poutre ou de la force qui les sépare. Les différentes contraintes s'exerçant autour d'une région permettent de situer le point la représentant par construction géométrique (intersection de droites). Les segments sont en fait les forces s'exerçant sur les poutres représentées à l'échelle.

Par rapport au diagramme ci-contre, on a :

• force 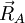 : segment 1–3 ;
• force 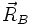 : segment 3–2 ;
• force 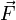 : segment 2–1 ;
• forces de traction dans l'élément A–B : segment 3–4 ;
• forces de compression dans l'élément B–C : segment 2–4 ;
• forces de compression dans l'élément A–C : segment 1–4.

En connaissant le module des forces extérieures ( 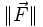est donné, 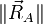et 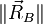sont calculées par la statique), la construction permet de mesurer, ou de calculer par trigonométrie, les forces de traction ou de compression dans les poutres à partir des seules orientations des poutres. On peut ainsi vérifier que les poutres résistent à la traction ou au flambage.

Principe

Formation des polygones pour construire le diagramme de Cremona

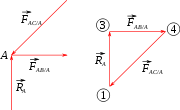
La structure est en équilibre. Cela signifie qu'à chaque nœud, la somme des forces est nulle. On peut donc tracer un polygone en mettant les forces bout à bout (le polygone des forces, encore appelé « polygone dynamique » ou simplement « le dynamique ») ; dans l'exemple présent, il s'agit de triangles puisqu'il n'y a que trois forces à chaque nœud. Chaque force correspond à une poutre qui sépare deux zones, chaque angle du triangle peut donc être étiqueté avec le nom de la zone commune aux deux forces qui constituent les côtés adjacent à cet angle.

Les différents triangles ainsi constitués pour chaque nœud peuvent être placée à la façon d'un puzzle, ce qui constitue le diagramme, ou épure, de Cremona.

Méthode

Les deux forces extérieures à une poutre sont opposées (condition d'équilibre) ; le dynamique de chaque nœud a donc un côté commun avec le dynamique de chaque nœud voisin. En mettant tous les dynamiques sur la même figure, on évite donc de devoir reporter des segments d'un dessin sur l'autre. Cependant, il faut procéder de manière méthodique afin que les dynamiques s'accolent bien.

La première étape consiste à découper le plan en régions, ou zones, séparées par des poutres ou des lignes d'action des forces extérieures. Ces zones sont numérotées, et les numéros désigneront les sommets du Cremona ; les directions des éléments (poutre ou force extérieure) seront les directions des segments de l'épure de Cremona.

Puis, on choisi un sens de rotation (par exemple le sens trigonométrique), et pour chaque nœud, on liste les zones en tournant dans le sens choisi ; on indique l'élément séparant chaque zone contiguë, et l'on reporte ceci dans un tableau. On prend ici pour valeur 100 N pour 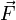, et donc 50 N pour 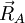et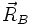

Liste des segments de l'épure

Nœud	Élément	Zones	Sollicitation	Intensité
A	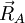	1→3		50 N
	AB	3→4	traction	?
	AC	4→1	compression	?
B	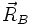	3→2		50 N
	BC	2→4	traction	?
	AB	4→3	compression	?
C	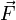	2→1		100 N
	AC	1→4	compression	?
	BC	4→2	traction	?

Les mentions « traction » ou « compression » sont obtenues par la « logique ».

On choisit une échelle pour les forces. Puis, on prend un nœud pour lequel on connaît une force et on trace son dynamique :

• en commençant par la force connue : on trace cette force sur le dynamique, et on donne aux extrémité les numéros indiqués sur la ligne du tableau ;
  par exemple, pour le nœud A, on commence par tracer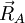 , on place le point 3 en bas du segment et le point 1 en haut (puisque 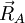va de bas en haut et va du 3 à 1) ;
• à partir de chaque extrémité, on trace la direction de l'élément qui part de cette extrémité ; l'intersection des segment permettent de trouver le troisième point ;
  par exemple, on part de 3 et on trace une horizontale (direction de AC, puisque AC relie 3 et 4), ensuite on part de 1 et on trace la parallèle à AB ; ceci nous donne le point 4.

On passe à un nœud contigu et on recommence ; un des côté du dynamique est commun avec le dynamique précédent.

La longueur des segments construits permet de déterminer l'intensité des forces en jeu dans les poutres correspondantes.

Voir aussi

Articles connexes

• Méthode de Ritter (méthode des sections)