Couplage (Théorie des Graph)

Couplage (Théorie des Graph)

Appariement (mathématiques)

Page d'aide sur l'homonymie Pour les articles homonymes, voir Appariement.

En théorie des graphes, un appariement ou couplage d'un graphe (en anglais matching) est un ensemble d'arêtes de ce graphe qui n'ont pas de sommets en commun.

Définitions

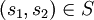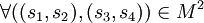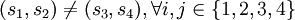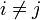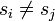Soit un graphe G = (S,A), l'appariement M est un ensemble d'arêtes non-adjacentes deux à deux. C'est à dire, M est l'ensemble des arêtes (s_1,s_2)\in S telles que \forall ((s_1,s_2), (s_3,s_4)) \in M^2 avec (s_1,s_2)\neq(s_3,s_4), \forall i,j \in \{1,2,3,4\}, avec i \neq j, alors s_i \neq s_j .

Un appariement maximum est un appariement contenant le plus grand nombre possible d'arêtes. Un graphe peut posséder plusieurs appariements maximum.

Un appariement maximal est un appariement M du graphe tel que toute arête du graphe possède une intersection non vide avec au moins une arête de M. Il en découle la propriété suivante : soit un appariement maximal M, si une arête quelconque de A qui n'est pas dans M est ajoutée à M , alors M n'est plus un appariement de G.

Un appariement parfait ou appariement complet est un appariement M du graphe tel que tout sommet du graphe est incident à exactement une arête de M.

Propriétés

Un appariement maximum est aussi un appariement maximal.

Un appariement parfait est aussi un appariement maximal.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Appariement (math%C3%A9matiques) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Couplage (Théorie des Graph) de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Theoreme de Konig (theorie des graphes) — Théorème de König (théorie des graphes) En théorie des graphes, un couplage d un graphe G est un sous ensemble d arêtes de G deux à deux non adjacentes. Un transversal de G est un sous ensemble de sommets T de G avec la propriété que toute arête… …   Wikipédia en Français

  • Théorème de könig (théorie des graphes) — En théorie des graphes, un couplage d un graphe G est un sous ensemble d arêtes de G deux à deux non adjacentes. Un transversal de G est un sous ensemble de sommets T de G avec la propriété que toute arête de G est incidente à au moins un sommet… …   Wikipédia en Français

  • Théorème de König (théorie des graphes) — Pour les articles homonymes, voir Théorème de König. En théorie des graphes, un couplage d un graphe G est un sous ensemble d arêtes de G deux à deux non adjacentes. Un transversal de G est un sous ensemble de sommets T de G avec la propriété que …   Wikipédia en Français

  • Problème des ménages —  Ne doit pas être confondu avec Lemme des mariages. Une table à dix couverts. D après la solution au problème des ménages, il y a 3120 manières différentes, pour 5 couples, de s asseoir en alternant hommes et femmes et sans qu aucu …   Wikipédia en Français

  • Théorème de Hall —  Ne pas confondre avec le théorème de Hall en théorie des groupes, ni avec le problème des ménages. En mathématiques, le théorème de Hall ou lemme des mariages est un résultat combinatoire qui donne une condition nécessaire et suffisante,… …   Wikipédia en Français

  • Graphe planaire extérieur — Un graphe planaire extérieur maximal, muni d un 3 coloriage. En mathématiques, et plus particulièrement en théorie des graphes, un graphe non orienté est planaire extérieur (ou, par calque de l anglais, outer planar) s il peut être dessiné dans… …   Wikipédia en Français

  • Théoreme de Hall — Théorème de Hall Le théorème de Hall donne une condition nécessaire et suffisante à l existence d un couplage parfait dans un graphe biparti (un couplage parfait dans un graphe ayant un nombre pair 2n de sommets est un sous ensemble de n arêtes… …   Wikipédia en Français

  • Théorème de hall — Le théorème de Hall donne une condition nécessaire et suffisante à l existence d un couplage parfait dans un graphe biparti (un couplage parfait dans un graphe ayant un nombre pair 2n de sommets est un sous ensemble de n arêtes deux à deux… …   Wikipédia en Français

  • ATOME — L’atome est le terme ultime de la division de la matière dans lequel les éléments chimiques conservent leur individualité. C’est la plus petite particule d’un élément qui existe à l’état libre ou combiné. On connaît 89 éléments naturels auxquels… …   Encyclopédie Universelle

  • Problème du postier chinois — En théorie des graphes, le problème du postier chinois consiste à trouver un plus court chemin dans un graphe connexe non orienté qui passe au moins une fois par chaque arête du graphe et revient à son point de départ. Le nom du problème vient du …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”