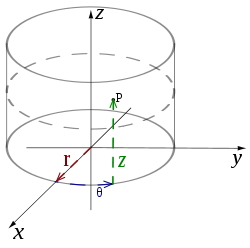
Coordonnées cylindriques

Coordonnées cylindriques
En coordonnées cylindriques, la position du point P est définie par les distances r et Z et par l'angle θ.

Le système de coordonnées cylindriques est un système de coordonnées qui étend le système de coordonnées polaires à deux dimensions en y ajoutant une troisième dimension qui mesure la hauteur d'un point par rapport au plan repéré par les coordonnées polaires; de la même manière que l'on étend le système de coordonnées cartésiennes de deux à trois dimensions. La troisième coordonnée est souvent notée h ou z.

Conversion entre système cartésien et cylindrique

À partir des coordonnées cartésiennes (x,y,z), on peut obtenir les coordonnées cylindriques (r,θ,h) grâce aux formules suivantes :

\begin{align} r & = \sqrt{x^2 + y^2}\\ \theta & = \arctan\left({y \over x}\right) \\ h & = z \end{align}

On peut également convertir les coordonnées cylindriques (r,θ,h) en coordonnées cartésiennes (x,y,z) grâce aux formules suivantes :

\begin{align} x &= r \cos\theta \\ y &= r \sin\theta \\ z &= h \end{align}

Cinématique

Les coordonnées cylindriques sont notamment utilisées dans de nombreux problèmes de mécanique où l'on considère un objet dans un repère tournant. On peut alors avoir besoin des relations concernant la vitesse et l'accélération.

Pour \overrightarrow {u_r} un vecteur radial et \overrightarrow {u_\theta} un vecteur orthoradial, les quantités cinématiques, position, vitesse et accélération sont données par :

\begin{align} \overrightarrow{OM} &= r\overrightarrow{u_r} + z\overrightarrow{u_z}\\ \dot{\overrightarrow{OM}} &= \dot r\overrightarrow{u_r} + r\dot\theta\overrightarrow{u_\theta} + \dot z\overrightarrow{u_z}\\ \ddot{\overrightarrow{OM}} &= (\ddot r-r\dot\theta^2)\overrightarrow{u_r} + (r\ddot\theta+2\dot r\dot\theta)\overrightarrow{u_\theta} + \ddot z\overrightarrow{u_z}\\ \end{align}

Il est à noter que l'on peut retrouver ces résultats :

\begin{align} \dot{\overrightarrow{OM}} &= \frac {d\overrightarrow{OM}}{dt} = \frac {d(r\overrightarrow{u_r} + z\overrightarrow{u_z})}{dt} = \frac {d(r\overrightarrow{u_r})}{dt} + \frac {d(z\overrightarrow{u_z})}{dt}\\ \dot{\overrightarrow{OM}} &= \frac {d(r)}{dt} \overrightarrow{u_r} + r \frac {d(\overrightarrow{u_r})}{dt} + \frac {d(z)}{dt} \overrightarrow{u_z} + z \frac {d(\overrightarrow{u_z})}{dt} \\ \frac {d(r)}{dt} &= \dot r \quad \frac {d(\overrightarrow{u_r})}{dt}= \dot\theta\overrightarrow{u_\theta} \quad \frac {d(z)}{dt}=\dot z \quad \frac {d(\overrightarrow{u_z})}{dt}=\overrightarrow{0}\\ \end{align}

On retrouve donc l'expression de \dot{\overrightarrow{OM}}

Voir aussi


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Coordonnées cylindriques de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Coordonnees cylindriques — Coordonnées cylindriques Un point repéré en coordonnées cylindriques Le système de coordonnées cylindriques est un système de coordonnées qui étend le système de coordonnées polaires à deux dimensions en y ajoutant une troisième dimension qui… …   Wikipédia en Français

  • Coordonnées Cylindriques — Un point repéré en coordonnées cylindriques Le système de coordonnées cylindriques est un système de coordonnées qui étend le système de coordonnées polaires à deux dimensions en y ajoutant une troisième dimension qui mesure la hauteur d un point …   Wikipédia en Français

  • coordonnées cylindriques — cilindrinės koordinatės statusas T sritis automatika atitikmenys: angl. cylindrical coordinates vok. zylindrische Koordinaten, f rus. цилиндрические координаты, f pranc. coordonnées cylindriques, f …   Automatikos terminų žodynas

  • coordonnées cylindriques — cilindrinės koordinatės statusas T sritis fizika atitikmenys: angl. cylindrical coordinates vok. zylindrische Koordinaten, f rus. цилиндрические координаты, f pranc. coordonnées cylindriques, f …   Fizikos terminų žodynas

  • Système de coordonnées cylindriques — Coordonnées polaires Un cercle découpé en angles mesurés en degré Les coordonnées polaires sont, en mathématiques, un système de coordonnées à deux dimensions, dans lequel chaque point du plan est entièrement déterminé par un angle et une… …   Wikipédia en Français

  • Opérateurs nabla dans les coordonnées cylindriques et sphériques — Nabla Articles d analyse vectorielle Objets d étude …   Wikipédia en Français

  • système de coordonnées cylindriques — cilindrinė koordinačių sistema statusas T sritis fizika atitikmenys: angl. cylindrical co ordinates system vok. Zylinderkoordinatensystem, n rus. цилиндрическая система координат, f pranc. système de coordonnées cylindriques, m …   Fizikos terminų žodynas

  • Coordonnees polaires — Coordonnées polaires Un cercle découpé en angles mesurés en degré Les coordonnées polaires sont, en mathématiques, un système de coordonnées à deux dimensions, dans lequel chaque point du plan est entièrement déterminé par un angle et une… …   Wikipédia en Français

  • Coordonnées Polaires — Un cercle découpé en angles mesurés en degré Les coordonnées polaires sont, en mathématiques, un système de coordonnées à deux dimensions, dans lequel chaque point du plan est entièrement déterminé par un angle et une distance. Ce système est… …   Wikipédia en Français

  • Coordonnées polaires (Mathématiques) — Coordonnées polaires Un cercle découpé en angles mesurés en degré Les coordonnées polaires sont, en mathématiques, un système de coordonnées à deux dimensions, dans lequel chaque point du plan est entièrement déterminé par un angle et une… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”