Coordonnées barycentriques

Coordonnées barycentriques

En géométrie affine, les coordonnées barycentriques d'un point par rapport à un repère barycentrique sont une famille de poids permettant de définir ce point comme un barycentre.

Sommaire

Définition

Soit (P0,...,Pn) une famille de points dans un espace affine telle que chaque point ne puisse s'écrire comme le barycentre des autres points et qui ne soient pas tous contenus dans un sous-espace affine strict[1]. Une telle famille est appelée repère barycentrique et dans ce cas, n'importe quel point M de l'espace affine peut s'écrire comme un barycentre des points du repère :

\lambda_0 \cdot MP_0 + \lambda_1 \cdot MP_1 + ... + \lambda_n \cdot MP_n =0
Coordonnées barycentriques dans le triangle.

Les coordonnées barycentriques de n'importe quel point de l'espace sont alors les « poids » (λ0,...,λn) associés à chaque point du repère. Elles peuvent être définies de manière unique en supposant que la somme des poids soit fixée à 1.

Exemple : coordonnées dans un triangle

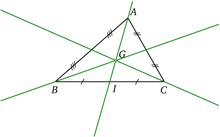
Étant donné un triangle ABC de centre de gravité G, le point G est de coordonnées barycentriques (1;1;1) par rapport au repère (A,B,C).

En notant I le milieu de [BC], G a pour coordonnées barycentriques (1;2) par rapport au repère (A,I) de la droite (AI).

Dans ce triangle, le point I est de coordonnées (0;1;1) par rapport au repère (A,B,C).

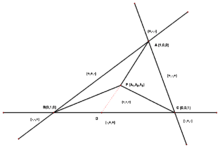
Interprétation des coordonnées barycentriques en termes de rapports de surfaces.

Coordonnées et aire. - P désignant un point du plan du triangle ABC (fig. ci-contre) extérieur aux trois droites (AB), (BC), (AC), de coordonnées barycentriques α1,α2,α3 (\alpha_1 \cdot PA + \alpha_2 \cdot PB + \alpha_3 \cdot PC =0 avec α1 + α2 + α3 = 1), ces coordonnées normalisées s'interprètent comme des rapports d'aires de la façon suivante :

\begin{cases} \alpha_1 = \frac{Aire(BPC)}{Aire(ABC)} \\ \alpha_2 = \frac{Aire(APC)}{Aire(ABC)} \\ \alpha_3 = \frac{Aire(BPA)}{Aire(ABC)} \end{cases}

Convexité

L'enveloppe convexe d'un ensemble de points E rassemble tous les points admettant des coordonnées barycentriques à coefficients tous positifs par rapport à une famille de points de E[2].

Lien avec les coordonnées cartésiennes

Dans un espace vectoriel muni d'une base (e1,...,en), la famille (0,e1,...,en) constitue un repère barycentrique pour la structure d'espace affine canonique et tout vecteur de composantes (λ1,...,λn) pour la base (e1,...,en), correspond au point de coordonnées barycentriques (1 − s,λ1,...,λn), où s est la somme des coefficients λi.

Notes et références

  1. ↑ Autrement dit, il faut qu'ils n'appartiennent pas tous à un même hyperplan.
  2. ↑ Marcel Berger, Géométrie [détail des éditions], Prop. 11.1.8.4, tome 3, p. 26 dans l'édition de 1978.

Lien externe


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Coordonnées barycentriques de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Coordonnées barycentriques d'un point M — ● Coordonnées barycentriques d un point M (n + 1) uple (a0, a1, …, an) de scalaires tels que M est le barycentre des n + 1 points A0, A1, …, An affectés de ces coefficients, étant un repère affine de l espace affine de référence …   Encyclopédie Universelle

  • coordonnées — [ kɔɔrdɔne ] n. f. pl. • 1754; de co et ordonnée 1 ♦ Math. Coordonnées d un point M :scalaires qui permettent de repérer ce point sur une courbe, une surface, dans un espace. Coordonnées dans le plan euclidien (dans R2), dans l espace euclidien… …   Encyclopédie Universelle

  • Coordonnées d'un point M — ● Coordonnées d un point M n uplet de réels (ou [n + 1] uplet dans les cas des coordonnées barycentriques et des coordonnées homogènes) qui servent à déterminer la position du point M dans l espace affine En de dimension n …   Encyclopédie Universelle

  • Axiomes De Plans Projectifs/barycentriques — Article principal : Axiomes de plans projectifs. La notion de plan projectif barycentrique (PPB) est facile à imaginer intuitivement. Elle se définit à partir de la notion de barycentre dans un plan très ordinaire auquel on rajoute des… …   Wikipédia en Français

  • Axiomes de plans projectifs/barycentriques — Article principal : Axiomes de plans projectifs. La notion de plan projectif barycentrique (PPB) est facile à imaginer intuitivement. Elle se définit à partir de la notion de barycentre dans un plan très ordinaire auquel on rajoute des… …   Wikipédia en Français

  • Coordonnee barycentrique — Coordonnées barycentriques En géométrie affine, les coordonnées barycentriques d un point par rapport à un repère barycentrique est une famille de poids permettant de définir ce point comme un barycentre. Sommaire 1 Définition 2 Exemple 3… …   Wikipédia en Français

  • Coordonnée Barycentrique — Coordonnées barycentriques En géométrie affine, les coordonnées barycentriques d un point par rapport à un repère barycentrique est une famille de poids permettant de définir ce point comme un barycentre. Sommaire 1 Définition 2 Exemple 3… …   Wikipédia en Français

  • Coordonnée barycentrique — Coordonnées barycentriques En géométrie affine, les coordonnées barycentriques d un point par rapport à un repère barycentrique est une famille de poids permettant de définir ce point comme un barycentre. Sommaire 1 Définition 2 Exemple 3… …   Wikipédia en Français

  • Repère barycentrique — Coordonnées barycentriques En géométrie affine, les coordonnées barycentriques d un point par rapport à un repère barycentrique est une famille de poids permettant de définir ce point comme un barycentre. Sommaire 1 Définition 2 Exemple 3… …   Wikipédia en Français

  • Barycentre (Géométrie Euclidienne) — Pour les articles homonymes, voir Barycentre. En géométrie, le barycentre est un point qui permet de résumer un ensemble géométrique sur lequel sont réparties des valeurs numériques. Ces valeurs peuvent représenter des poids pour déterminer le… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”