Contrainte non holonome

Contrainte non holonome

Contrainte holonome

En mécanique analytique, on dit qu'un système de N particules est soumis à une contrainte holonome s'il existe une fonction 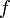\ f telle que les vecteurs coordonnées 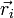\vec r_i des particules, pour 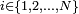\scriptstyle i \in \{ 1,2,...,N \}, vérifient 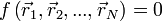\ f \left( \vec r_1 , \vec r_2,..., \vec r_N \right) =0. Si les contraintes sont modélisées par un système d'équations de ce type, on parle encore de contraintes holonomes.

Une contrainte qui ne peut pas s'écrire sous cette forme est dite non holonome.

Si l'équation de la contrainte holonome dépend du temps, 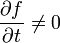\frac{\partial f}{\partial t} \ne 0, elle est dite rhéonome, si elle n'en dépend pas, 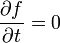\frac{\partial f}{\partial t} = 0, elle est dite scléronome.

Mathématiquement, une contrainte holonome définit une variété fermée plongée dans l'espace 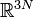\textstyle \R^{3N} dans laquelle évolue le système de particules. La dimension de cette variété est le nombre de degrés de liberté du système et le nombre de coordonnées indépendantes à considérer pour le décrire. En général K contraintes holonomes enlèvent K degrés de liberté, mais, suivant les équations et leur indépendance, il peut en être autrement (on peut ramener K équations indépendantes à une seule équation si on le souhaite ; ce sujet dans toute sa généralité relève de la géométrie algébrique).

Sommaire

Exemple

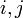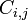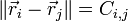La rigidité d'un corps supposé rigide est un ensemble de contraintes holonomes scléronomes : pour deux particules quelconques numérotées \ i,j, il existe une constante \ C_{i,j} telle que l'on doit avoir \| \vec r_i -\vec r_j \| = C_{i,j}.

Coordonnées généralisées

  • Un système de N corps ponctuels non soumis à une contrainte holonome a 3N degrés de liberté et nécessite donc 3N variables réelles indépendantes pour être décrit (par exemple : les 3N coordonnées des N corps).
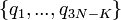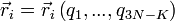  • Un système de N corps ponctuels soumis à une contrainte holonome a 3N-K degrés de liberté et nécessite donc 3N-K variables réelles indépendantes pour être décrit : ce peut être des coordonnées spatiales de certains corps, ou d'autres données. Dans ce dernier cas on parle de « coordonnées généralisées » que l'on note \ \{q_1 , ... , q_{3N-K} \} et on a \vec r_i = \vec r_i \left( q_1 , ... , q_{3N-K} \right).

Dans l'espace, un triangle est déterminé par trois sommets (donc 9 coordonnées) soumis à trois contraintes holonomes indépendantes (les 3 contraintes de longueurs), donc il y a 9-3 = 6 degrés de liberté. Dans l'espace un triangle est donc déterminé par 6 variables indépendantes (on peut choisir les 3 coordonnées d'un des sommets et 3 angles qui permettent de déterminer les directions de deux côtés). La position de tout solide rigide est déterminée par trois de ses points non-alignés quelconques, donc elle est aussi déterminée par 6 variables indépendantes.

Déplacement virtuel, forces de contrainte et principe de d'Alembert

Un déplacement virtuel 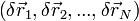\left( \delta \vec r_1 , \delta \vec r_2 , ... , \delta \vec r_N \right) est un déplacement instantanné et infinitésimal du système de telle sorte qu'il vérifie toujours ses contraintes. Pour une contrainte holonome, on doit donc avoir 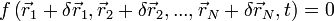\ f \left( \vec r_1 + \delta \vec r_1 , \vec r_2 + \delta \vec r_2 , ... 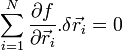, \vec r_N + \delta \vec r_N , t \right) = 0, d'où, au premier ordre, \sum_{i=1}^{N}\frac{\partial f}{\partial \vec r_i}.\delta \vec r_i = 0.

Le principe de d'Alembert postule que les 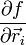\frac{\partial f}{\partial \vec r_i} sont proportionnels aux forces de contrainte 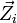\vec Z_i de la contrainte 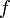\ f (ce sont les forces dans 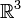\R^{3} qui obligent le système à respecter cette contrainte) et donc que le travail de ces forces de contrainte dans un déplacement virtuel est nul :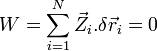 W = \sum_{i=1}^{N} \vec Z_i.\delta \vec r_i = 0

Exemples de contraintes non holonomes

  • Un corps M ponctuel dont les mouvement sont limités à l'intérieur d'une sphère de centre O et de rayon R vérifie l'inéquation 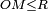\scriptstyle OM \le R, soit 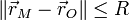\textstyle \| \vec r_M - \vec r_O \| \le R , ce qui est une contrainte non-holonome.
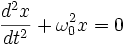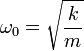  • Une masse ponctuelle attachée à l'extrémité d'un ressort vérifie la contrainte non-holonome \frac{d^2x}{dt^2}+\omega_0^2 x = 0, avec \omega_0 = \sqrt{\frac{k}{m}}.
  • Un système vérifiant la contrainte holonome 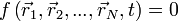\ f \left( \vec r_1 , \vec r_2,..., \vec r_N , t \right) =0 vérifie aussi 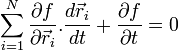\sum_{i=1}^{N}\frac{\partial f}{\partial \vec r_i}.\frac{d \vec r_i}{d t} + \frac{\partial f}{\partial t} = 0, ce qui est une contrainte non holonome, obtenue en dérivant par \ t.

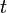Bibliographie

  • Mécanique analytique par Rossen Dandoloff aux éditions Publibook, 2005, 126 pages ISBN 9782748307788.
  • Claude Gignoux et Bernard Silvestre-Brac ; Mécanique : de la formulation lagrangienne au chaos hamiltonien, éditeur EDP-Sciences, 2002, 467 pages ISBN 2868835848.
  • Portail de la physique Portail de la physique
Ce document provient de « Contrainte holonome ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Contrainte non holonome de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • contrainte non holonome — neholonominis ryšys statusas T sritis fizika atitikmenys: angl. non holonomic constraint vok. nichtholonome Bindung, f rus. неголономная связь, f pranc. contrainte anholonome, f; contrainte non holonome, f; liaison non holonome, f …   Fizikos terminų žodynas

  • liaison non holonome — neholonominis ryšys statusas T sritis fizika atitikmenys: angl. non holonomic constraint vok. nichtholonome Bindung, f rus. неголономная связь, f pranc. contrainte anholonome, f; contrainte non holonome, f; liaison non holonome, f …   Fizikos terminų žodynas

  • Holonome — Contrainte holonome En mécanique analytique, on dit qu un système de N particules est soumis à une contrainte holonome s il existe une fonction telle que les vecteurs coordonnées des particules, pour , vérifient . Si les contraintes sont… …   Wikipédia en Français

  • Contrainte holonome — En mécanique analytique, on dit qu un système de N particules est soumis à une contrainte holonome s il existe une équation algébrique caractérisant l état du système : équation algébrique de plusieurs variables que sont les vecteurs… …   Wikipédia en Français

  • contrainte anholonome — neholonominis ryšys statusas T sritis fizika atitikmenys: angl. non holonomic constraint vok. nichtholonome Bindung, f rus. неголономная связь, f pranc. contrainte anholonome, f; contrainte non holonome, f; liaison non holonome, f …   Fizikos terminų žodynas

  • non-holonomic constraint — neholonominis ryšys statusas T sritis fizika atitikmenys: angl. non holonomic constraint vok. nichtholonome Bindung, f rus. неголономная связь, f pranc. contrainte anholonome, f; contrainte non holonome, f; liaison non holonome, f …   Fizikos terminų žodynas

  • neholonominis ryšys — statusas T sritis fizika atitikmenys: angl. non holonomic constraint vok. nichtholonome Bindung, f rus. неголономная связь, f pranc. contrainte anholonome, f; contrainte non holonome, f; liaison non holonome, f …   Fizikos terminų žodynas

  • nichtholonome Bindung — neholonominis ryšys statusas T sritis fizika atitikmenys: angl. non holonomic constraint vok. nichtholonome Bindung, f rus. неголономная связь, f pranc. contrainte anholonome, f; contrainte non holonome, f; liaison non holonome, f …   Fizikos terminų žodynas

  • неголономная связь — neholonominis ryšys statusas T sritis fizika atitikmenys: angl. non holonomic constraint vok. nichtholonome Bindung, f rus. неголономная связь, f pranc. contrainte anholonome, f; contrainte non holonome, f; liaison non holonome, f …   Fizikos terminų žodynas

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”