Construction des entiers relatifs

Construction des entiers relatifs
Article principal : Entier relatif.

Le but de cet article est de:

  • construire l'ensemble \mathbb{Z} des entiers relatifs,
  • construire une structure de groupe sur cet ensemble,
  • montrer que cela prolonge le monoïde (additif) des entiers naturels,

La structure d'anneau sera juste esquissée.

Sommaire

Construction de l'ensemble \mathbb{Z}

Représentation des classes d'équivalence pour les nombres de -5 à 5
Les points rouges représentent les couples d'entiers modélisant les relatifs. Les points rouges reliés par des pointillés bleus appartiennent à la classe d'équivalence du nombre relatif situé dans le prolongement de la ligne, lui aussi en bleu.

On sait déjà que l'ensemble des entiers naturels \mathbb{N}, muni de l'opération interne addition, est un monoïde commutatif ; donc notre but est simplement de rajouter un opposé (inverse pour l'addition) pour chaque entier non nul. Il ne s'agit pas de rajouter brutalement un élément, il faut aussi se donner les moyens de définir l'addition sans douleur !

C'est pourquoi on va partir de la notion naïve d'entier relatif, que l'on suppose déjà connue, pour construire l'objet mathématique correspondant. Si on veut définir − 2 avec des entiers naturels, on a envie de le voir comme 0 − 2, ou comme 5 − 7, ou ... ; bref, on a envie de le voir comme la différence de deux entiers naturels. Cela pose une difficulté, car on voit d'une part que l'écriture n'est pas unique, et d'autre part, que cela fait intervenir une opération, la soustraction, qui n'a aucun sens avec les entiers naturels.

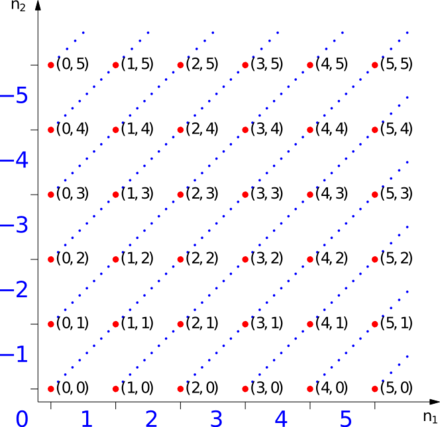
On va donc considérer des paires d'entiers, de la forme (n1,n2), et considérer que la paire (n1,n2) correspond à l'entier relatif naïf n1 − n2; et comme on a vu qu'il n'est pas raisonnable de prendre \mathbb{N}\times\mathbb{N} comme ensemble des entiers relatifs, on va regrouper les paires qui correspondent au même entier relatif naïf.

Pour cela, on va définir sur \mathbb{N}\times\mathbb{N} une relation d'équivalence R, par la relation suivante: (n_1,n_2)R(n_1',n_2')\Leftrightarrow n_1+n_2'=n_1'+n_2. Notez qu'intuitivement on est en train d'écrire que deux couples sont égaux si quand on soustrait le second de la paire au premier on obtient le même entier naturel ! Mais on n'utilise que la somme pour définir R, donc cette définition n'utilise pas d'objet naïf.

Les relations d'équivalences sont faites pour quotienter; on définit donc: \mathbb{Z}=(\mathbb{N}\times\mathbb{N})/R

Définition de la structure de groupe

On dispose maintenant de l'ensemble des entiers relatifs; il reste à définir l'addition sur ces derniers: pour cela, on ne dispose que de la définition sur les entiers; on va donc d'abord définir une opération sur les paires d'entiers, et comme elle sera compatible avec la relation R, elle donnera une opération sur les entiers relatifs!

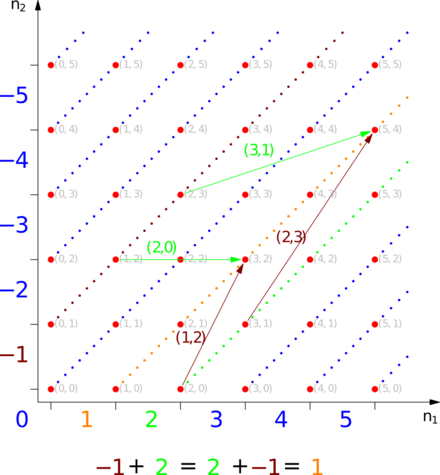
On définit la somme de deux paires d'entier ainsi: (n1,n2) + (n1',n2') = (n1 + n1',n2 + n2'); cette opération est visiblement déjà commutative, associative et d'élément neutre (0,0) sur les paires d'entiers; elle passe clairement au quotient, pour donner sur \mathbb{Z} une structure de monoïde commutative.

Il ne reste donc qu'à trouver un opposé à tout entier relatif; mais ceci est immédiat: si (n1,n2) représente un entier relatif dans les paires d'entiers, on a (n1,n2) + (n2,n1) = (n1 + n2,n1 + n2) où (n1 + n2,n1 + n2) est équivalent à (0,0), donc la classe d'équivalence de (n2,n1) est opposée à la classe d'équivalence de (n1,n2)...

Représentation vectorielle de l'addition de deux entiers relatifs (2 et -1) sous différentes formes.
Addition de 2 et de -1, ainsi que de -1 et de 2 avec différents représentants.
Représentation vectorielle de l'addition de deux opposés (2 et -2) sous différentes formes.
Addition de 2 et de -2, ainsi que de -2 et de 2 avec différents représentants.

Vérification du prolongement

On va montrer qu'il y a un morphisme de monoïdes injectif de \mathbb{N} dans \mathbb{Z}; de cette façon, on pourra voir un entier naturel comme un cas particulier d'entier relatif. À nouveau, c'est l'idée naïve que l'on se faisait des entiers relatifs qui montre la voie.

Soit n un entier naturel; on lui associe la classe de la paire (n,0). On voit alors que:

  • 0 a pour image la classe de (0,0), donc le 0 des entiers relatifs;
  • n + n', la somme de deux entiers, a pour image la classe de (n + n',0), qui est la somme des classes de (n,0) et (n',0).

par ailleurs, on voit bien que cette application est injective, puisque demander que les classes de (n,0) et (n',0) soient égales, c'est justement demander que n = n'!

Écriture simplifiée des éléments de Z

Tout couple d'entiers naturels (n ; m) se trouve dans l'un de ces trois types de classes

  • une classe (d ; 0) si n > m avec n = m + d et d non nul
  • une classe (0 ; d) si n < m avec n + d = m et d non nul
  • la classe (0 ; 0) si n = m

Or l'ensemble des classes (d ; 0) est isomorphe à \mathbb{N}, on note donc ces classes sous la forme simplifiée d.

D'autre part, pour d non nul, les classes (d ; 0) et (0 ; d) sont opposées. En effet, (d ; 0) + (0 ; d) = (d ; d) = (0 ; 0) en termes de classes. On note donc les classes (0 ; d) sous la forme simplifiée (- d).

L'ensemble \mathbb{Z} retrouve alors sa forme plus classique de \mathbb{N} \cup \{(-d) /d \in \mathbb{N}^*\}.

Définition de la multiplication

On peut alors définir la multiplication comme suit: (n_1,n_2) \times (m_1,m_2) = (n_1 m_1 + n_2 m_2, n_1 m_2 + m_1 n_2) (toujours en s'inspirant de l'analogie avec les entiers relatifs naïfs).

Cette opération définie sur \mathbb{N}\times \mathbb{N} est associative, commutative, possède un élément neutre (1 ; 0) et est distributive pour l'addition précédemment établie. De plus elle est compatible avec la relation d'équivalence. Par passage au quotient, elle confère à \mathbb{Z} une structure d'anneau unitaire.

Les égalités

(d ; 0) \times (d';0) = (dd';0)
(d ; 0) \times (0;d') = (0;dd')
(0 ; d) \times (0;d') = (dd';0)

permettent les écritures

d \times d = dd'
d \times (-d') = (- dd')
(- d) \times (-d') = dd'

Cette écriture permet de prouver que l'anneau est aussi intègre.


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Construction des entiers relatifs de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Construction Des Entiers Relatifs — Le but de cet article est de: construire comme un ensemble, construire une structure de groupe sur cet ensemble, montrer que cela prolonge le monoïde (additif) des entiers naturels, La structure d anneau sera juste esquissée. Sommaire 1… …   Wikipédia en Français

  • Construction entiers relatifs — Construction des entiers relatifs Le but de cet article est de: construire comme un ensemble, construire une structure de groupe sur cet ensemble, montrer que cela prolonge le monoïde (additif) des entiers naturels, La structure d anneau sera… …   Wikipédia en Français

  • Entiers relatifs — Entier relatif Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier relatif (ou entier rationnel) est un nombre entier (c est à dire sans partie fractionnaire) et muni d un signe positif ( + ) ou négatif ( − ). L… …   Wikipédia en Français

  • Construction Des Nombres Rationnels — Objectif On veut construire le corps des nombres rationnels, à la fois comme ensemble et les structures supplémentaires. Construction Elle est très facile dans la mesure où l on connaît assez de théorie sur les anneaux : l anneau des entiers …   Wikipédia en Français

  • Construction des nombres rationnels — En mathématiques, plus précisément en algèbre, la construction des nombres rationnels consiste à définir l ensemble des nombres rationnels et à le munir d une structure de corps commutatif. Construction Article détaillé : Corps des fractions …   Wikipédia en Français

  • Construction des nombres réels — En mathématiques, il existe différentes constructions des nombres réels, dont les deux plus connues sont les coupures de Dedekind, les suites de Cauchy. Sommaire 1 Construction intuitive à partir des nombres décimaux 2 Construction par les… …   Wikipédia en Français

  • Idéal de l'anneau des entiers d'un corps quadratique — En mathématiques et plus précisément en théorie algébrique des nombres, l anneau des entiers d un corps quadratique ressemble à certains égards à celui des entiers relatifs. Certains d entre eux sont euclidiens comme celui des entiers de Gauss d… …   Wikipédia en Français

  • Entiers — Entier relatif Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier relatif (ou entier rationnel) est un nombre entier (c est à dire sans partie fractionnaire) et muni d un signe positif ( + ) ou négatif ( − ). L… …   Wikipédia en Français

  • Construction (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le mot construction peut désigner différentes notions. Sommaire 1 Construction à caractère matériel 2 …   Wikipédia en Français

  • Construction nombres rationnels — Construction des nombres rationnels Objectif On veut construire le corps des nombres rationnels, à la fois comme ensemble et les structures supplémentaires. Construction Elle est très facile dans la mesure où l on connaît assez de théorie sur les …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”