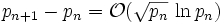Conjecture de Cramer
- Conjecture de Cramer
-
Conjecture de Cramér
En mathématiques, la conjecture de Cramér, formulée par le mathématicien suédois Harald Cramér en 1936, énonce que
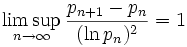
où pn est le n-ième nombre premier ; cette conjecture n'est pas démontrée à ce jour. Cramér a aussi formulé une autre conjecture concernant les nombres premiers, énonçant que
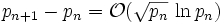
qu'il a démontrée sous l'hypothèse de Riemann (qui elle-même n'est pas encore démontrée non plus).
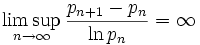 quant à elle est démontrée comme vraie.
quant à elle est démontrée comme vraie.
 Portail des mathématiques
Portail des mathématiques
Catégories : Théorie des nombres | Conjecture
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Conjecture de Cramer de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Conjecture De Cramér — En mathématiques, la conjecture de Cramér, formulée par le mathématicien suédois Harald Cramér en 1936, énonce que où pn est le n ième nombre premier ; cette conjecture n est pas démontrée à ce jour. Cramér a aussi formulé une autre… … Wikipédia en Français
Conjecture de cramér — En mathématiques, la conjecture de Cramér, formulée par le mathématicien suédois Harald Cramér en 1936, énonce que où pn est le n ième nombre premier ; cette conjecture n est pas démontrée à ce jour. Cramér a aussi formulé une autre… … Wikipédia en Français
Conjecture de Cramér — En mathématiques, la conjecture de Cramér, formulée par le mathématicien suédois Harald Cramér en 1936[1], pronostique que où pn est le n ième nombre premier et désigne le O de Landau ; cette conjecture n est pas démontrée à ce jour … Wikipédia en Français
Conjecture de Legendre — La conjecture de Legendre, proposée par Adrien Marie Legendre, énonce qu il existe un nombre premier entre n2 et (n+1)2 pour tout entier n. Cette conjecture est l un des problèmes de Landau, et n a pas été résolue à l heure actuelle (2011).… … Wikipédia en Français
Cramér's conjecture — In number theory, Cramér s conjecture, formulated by the Swedish mathematician Harald Cramér in 1936,[1] states that where pn denotes the nth prime number, O is big O notation, and log is the natural logarithm. Intuitively, this means the gaps… … Wikipedia
Harald Cramér — Pour les articles homonymes, voir Cramer. Harald Cramér Harald Cramér, né le 25 septembre 1893 et mort le 5 octobre 1985, e … Wikipédia en Français
Harald Cramer — Harald Cramér Pour les articles homonymes, voir Cramer. Harald Cramér Harald Cramér, né le 25 septembre 1893 et mort … Wikipédia en Français
Harald Cramér — Born 25 September 1893(1893 09 25) Stockholm, Sweden … Wikipedia
Twin prime conjecture — The twin prime conjecture is a famous unsolved problem in number theory that involves prime numbers. It states:: There are infinitely many primes p such that p + 2 is also prime. Such a pair of prime numbers is called a prime twin. The conjecture … Wikipedia
Andrica's conjecture — (named after Dorin Andrica) is a conjecture regarding the gaps between prime numbers. [ D. Andrica, Note on a conjecture in prime number theory. Studia Univ. Babes Bolyai Math. 31 (1986), no. 4, 44 48. ] The conjecture states that the inequality … Wikipedia
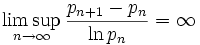 quant à elle est démontrée comme vraie.
quant à elle est démontrée comme vraie.