Conjecture De Vandiver

Conjecture de Vandiver

La conjecture de Vandiver concerne une propriété des corps de nombres algébriques. Bien qu'attribuée au mathématicien américain Harry Vandiver^[1] (1882 – 1973), la conjecture a été formulée en premier dans une lettre d'Ernst Kummer à Leopold Kronecker.

Soit 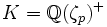$K=\mathbb{Q}(\zeta_p)^+$ , le sous-corps réel maximal du p-ième corps cyclotomique. La conjecture de Vandiver affirme que p ne divise pas le nombre de classes h_K de K.

Par comparaison, voir l'article sur les nombres premiers réguliers et irréguliers.

Une démonstration de la conjecture de Vandiver constituerait une avancée remarquable en théorie algébrique des nombres. Beaucoup de théorèmes reposent en effet sur la validité de cette conjecture. Par exemple, la conjecture de Vandiver entraîne que le p-rang du groupe de classes d'idéaux de 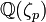$\mathbb{Q}(\zeta_p)$ est égal au nombre de nombres de Bernoulli divisibles par p (une amélioration remarquable du théorème de Herbrand-Ribet).

La conjecture de Vandiver a été vérifiée pour p inférieur à 12 millions^[2].

Sources

Cet article a été traduit de l'article anglais Vandiver's conjecture, qui incluait des passages de l'article de PlanetMath sous GFDL.

Bibliographie

(en) Lawrence C. Washington, Introduction to cyclotomic fields [détail des éditions]
E. Ghate, Vandiver's Conjecture via K-theory, 1999 - un examen du travail par Soulé et Kurihara - (DVI file) http://www.math.tifr.res.in/~eghate/vandiver.dvi

Portail des mathématiques

Ce document provient de « Conjecture de Vandiver ».

Catégories : Conjecture | Corps cyclotomiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Conjecture De Vandiver de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Conjecture de vandiver — La conjecture de Vandiver concerne une propriété des corps de nombres algébriques. Bien qu attribuée au mathématicien américain Harry Vandiver[1] (1882 – 1973), la conjecture a été formulée en premier dans une lettre d Ernst Kummer à Leopold… … Wikipédia en Français
Conjecture de Vandiver — La conjecture de Vandiver concerne une propriété des corps de nombres algébriques. Bien qu attribuée au mathématicien américain Harry Vandiver (en)[1] (1882 – 1973), la conjecture a été formulée en premier dans une lettre d Ernst Kummer à… … Wikipédia en Français
Conjecture De Greenberg — La conjecture de Greenberg porte sur la théorie algébrique des nombres, et plus particulièrement la théorie d Iwasawa. Elle a été énoncée par le mathématicien américain Ralph Greenberg, qui fut élève de Kenkichi Iwasawa, dans les années 1970.… … Wikipédia en Français
Conjecture de greenberg — La conjecture de Greenberg porte sur la théorie algébrique des nombres, et plus particulièrement la théorie d Iwasawa. Elle a été énoncée par le mathématicien américain Ralph Greenberg, qui fut élève de Kenkichi Iwasawa, dans les années 1970.… … Wikipédia en Français
Conjecture de Greenberg — La conjecture de Greenberg porte sur la théorie algébrique des nombres, et plus particulièrement la théorie d Iwasawa. Elle a été énoncée par le mathématicien américain Ralph Greenberg, qui fut élève de Kenkichi Iwasawa, dans les années 1970.… … Wikipédia en Français
Vandiver's conjecture — In mathematics, Vandiver s conjecture concerns a property of algebraic number fields. Although attributed to American mathematician Harry Vandiver, [MacTutor Biography|id=Vandiver|title=Henry Schultz Vandiver] the conjecture was first made in a… … Wikipedia
Harry Vandiver — Harry Schultz Vandiver (21 October, 1882 ndash; 9 January, 1973) was an American mathematician, known for work in number theory.He was born in Philadelphia, Pennsylvania to John Lyon and Ida Frances (Everett) Vandiver. He did not complete a… … Wikipedia
Corps cyclotomique — Extension cyclotomique En théorie algébrique des nombres, on appelle extension cyclotomique du corps des nombres rationnels, les surcorps de la forme où ζn est une racine primitive nème de l unité ; cette appellation provient de ce que ces… … Wikipédia en Français
Extension Cyclotomique — En théorie algébrique des nombres, on appelle extension cyclotomique du corps des nombres rationnels, les surcorps de la forme où ζn est une racine primitive nème de l unité ; cette appellation provient de ce que ces extensions sont des… … Wikipédia en Français
Extension cyclotomique — En théorie algébrique des nombres, on appelle extension cyclotomique du corps Q des nombres rationnels tout corps de rupture d un polynôme cyclotomique, i.e. tout corps de la forme Q(ζ) où ζ est une racine de l unité. Ces corps jouent un rôle… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Conjecture De Vandiver