Compacité (Cristallographie)

Compacité (Cristallographie)

Compacité (cristallographie)

Page d'aide sur l'homonymie Pour les articles homonymes, voir Compacité.

En cristallographie, la compacité (ou taux de remplissage) d'un édifice cristallin, dans le modèle des sphères dures, est le rapport du volume total des sphères d'une maille à celui de la maille qui les contient. C'est le taux d'occupation réel de l'espace.

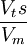
La compacité est donnée par \frac{V_ts}{V_m}

Exemple de calcul de compacité

Dans le cas d'un réseau cubique centré, par exemple, les sphères sont situées sur chacun des sommets du cube plus une au centre. On a donc huit fois un huitième de sphère (étant donné qu'un sommet est partagé entre huit cubes) plus une sphère complète. Le volume total des sphères est donc égal au volume de deux sphères, soit 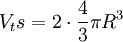V_ts=2\cdot \frac43 \pi R^3, où R est le rayon.

Le volume de la maille est donné par Vm = a3, où a est l'arrête du cube.

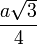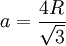R vaut \frac{a\sqrt{3}}{4} d'où l'on tire que a=\frac{4R}{\sqrt{3}}.

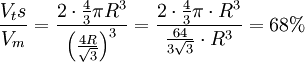
La compacité du réseau cubique centré vaut donc \frac{V_ts}{V_m}=\frac{2\cdot \frac43 \pi R^3}{\left(\frac{4R}{\sqrt{3}}\right)^3}=\frac{2\cdot \frac43 \pi \cdot R^3}{\frac{64}{3\sqrt{3}}\cdot R^3}=68%

Empilement compact ou non

Dans un empilement compact, par définition, la compacité est maximale et égale à 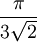\frac{\pi}{3 \sqrt{2}}. Il existe un lien direct entre la compacité d'un cristal et sa masse volumique, donc sa densité.

On peut calculer la compacité dans des cas simples, comme les deux cas d'empilements compacts que sont les réseaux hexagonal compact et cubique face centrée. Dans les deux cas, la compacité vaut 74%. Pour une structure diamant la compacité vaut 34%

Voir aussi

  • Portail de la chimie Portail de la chimie
Ce document provient de « Compacit%C3%A9 (cristallographie) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Compacité (Cristallographie) de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Compacite (cristallographie) — Compacité (cristallographie) Pour les articles homonymes, voir Compacité. En cristallographie, la compacité (ou taux de remplissage) d un édifice cristallin, dans le modèle des sphères dures, est le rapport du volume total des sphères d une… …   Wikipédia en Français

  • Compacité (cristallographie) — Pour les articles homonymes, voir Compacité. En cristallographie, la compacité (ou taux de remplissage) d un édifice cristallin, dans le modèle des sphères dures, est le rapport du volume total des sphères d une maille à celui de la maille qui… …   Wikipédia en Français

  • Compacite — Compacité Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La compacité est le caractère de ce qui est compact. Ce terme prend un sens particulier dans certains domaines : en topologie… …   Wikipédia en Français

  • Compacité — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La compacité est le caractère de ce qui est compact. Ce terme prend un sens particulier dans certains domaines : en topologie (mathématiques), voir… …   Wikipédia en Français

  • Atomic packing factor — Compacité (cristallographie) Pour les articles homonymes, voir Compacité. En cristallographie, la compacité (ou taux de remplissage) d un édifice cristallin, dans le modèle des sphères dures, est le rapport du volume total des sphères d une… …   Wikipédia en Français

  • Compacités — Compacité Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La compacité est le caractère de ce qui est compact. Ce terme prend un sens particulier dans certains domaines : en topologie… …   Wikipédia en Français

  • Empilement compact — L empilement compact est la manière d agencer des sphères dans l espace afin d avoir la plus grande densité de sphères, sans que celles ci ne se recouvrent. C est un problème que l on se pose en général en géométrie euclidienne dans l espace à… …   Wikipédia en Français

  • Empilement Compact — L empilement compact est la manière d agencer des sphères dans l espace afin d avoir la plus grande densité de sphères, sans que celles ci ne se recouvrent. C est un problème que l on se pose en général en géométrie euclidienne dans l espace à… …   Wikipédia en Français

  • Hexagonal compact — Empilement compact L empilement compact est la manière d agencer des sphères dans l espace afin d avoir la plus grande densité de sphères, sans que celles ci ne se recouvrent. C est un problème que l on se pose en général en géométrie euclidienne …   Wikipédia en Français

  • Clivage — Pour les articles homonymes, voir Clivage (homonymie). Le clivage est l aptitude de certains minéraux à se fracturer selon des surfaces planes dans des directions privilégiées lorsqu ils sont soumis à un effort mécanique (un choc ou une pression… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”