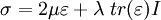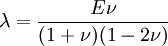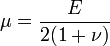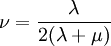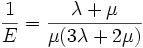Coefficients de lamé

Coefficients de Lamé

En mécanique des milieux continus, et plus précisément en élasticité linéraire, les coefficients de Lamé sont les deux coefficients suivants :

$λ$ , ou premier coefficient de Lamé
$μ$ , le module de cisaillement, aussi appelé second coefficient de Lamé

Ces deux coefficients sont homogènes à une contrainte et ont donc pour unité le Pascal (Pa).

Dans un matériau homogène, isotrope, satisfaisant la loi de Hooke en 3 dimensions :

$\sigma=2\mu \varepsilon +\lambda \; tr(\varepsilon)I$

Où $σ$ est le tenseur des contraintes, $ε$ le tenseur de déformation, $I$ le tenseur unité et 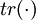$tr(\cdot)$ la trace. Voir aussi notation de Voigt.

Le premier paramètre $λ$ n'a pas d'interprétation physique, mais il sert à simplifier la matrice de raideur dans la loi de Hooke, ci-dessus. Les deux paramètres constituent un paramétrage des modules élastiques pour les matériaux homogènes isotropes, et sont donc liés aux autres modules. Selon les cas, on pourra choisir un autre paramétrage.

En particulier, les coefficients de Lamé s'expriment en fonction du module de Young $E$ et du coefficient de Poisson $ν$ :

$\lambda=\frac{E \nu}{(1+\nu)(1-2\nu)}$

$\mu = \frac{E}{2(1+\nu)}$

Et inversement :

$\nu = \frac {\lambda}{2(\lambda+\mu)}$

$\frac1E = \frac{\lambda+\mu}{\mu (3 \lambda + 2 \mu)}$

Les coefficients portent le nom de Gabriel Lamé.

Références

F. Kang, S. Zhong-Ci, Mathematical Theory of Elastic Structures, Springer New York, ISBN 0-387-51326-4, (1981)
G. Mavko, T. Mukerji, J. Dvorkin. The Rock Physics Handbook. Cambridge University Press 2003 (paperback). ISBN 0-521-54344-4

Portail de la physique

Ce document provient de « Coefficients de Lam%C3%A9 ».

Catégorie : Mécanique des milieux continus

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Coefficients de lamé de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Coefficients De Lamé — En mécanique des milieux continus, et plus précisément en élasticité linéraire, les coefficients de Lamé sont les deux coefficients suivants : λ, ou premier coefficient de Lamé μ, le module de cisaillement, aussi appelé second coefficient de … Wikipédia en Français
Coefficients de Lame — Coefficients de Lamé En mécanique des milieux continus, et plus précisément en élasticité linéraire, les coefficients de Lamé sont les deux coefficients suivants : λ, ou premier coefficient de Lamé μ, le module de cisaillement, aussi appelé… … Wikipédia en Français
Coefficients de Lamé — En mécanique des milieux continus, et plus précisément en élasticité linéaire, les coefficients de Lamé sont les deux coefficients suivants : λ, ou premier coefficient de Lamé ; μ, le module de cisaillement, aussi appelé second… … Wikipédia en Français
Coefficients De Fresnel — Pour les articles homonymes, voir Fresnel. Les coefficients de Fresnel, introduits par Augustin Jean Fresnel (1788 1827), interviennent dans la description du phénomène de réflexion réfraction des ondes électromagnétiques à l interface entre deux … Wikipédia en Français
Coefficients de fresnel — Pour les articles homonymes, voir Fresnel. Les coefficients de Fresnel, introduits par Augustin Jean Fresnel (1788 1827), interviennent dans la description du phénomène de réflexion réfraction des ondes électromagnétiques à l interface entre deux … Wikipédia en Français
Coefficients de Fresnel — Pour les articles homonymes, voir Fresnel. Amplitudes de réflexion et de transmission d une onde franchissant un dioptre vers un milieu d indice de réfraction supérieur. Les coefficients de Fresnel, i … Wikipédia en Français
Gabriel Lamé — Portrait de Gabriel Lamé Naissance (22 juillet 1795 … Wikipédia en Français
Fonctions de Lamé — En physique mathématique, Gabriel Lamé étudie l équilibre des températures dans les corps homogènes de forme ellipsoïdale et découvre en 1837 une équation différentielle, dont les solutions seront appelées les fonctions de Lamé . Mais Jacobi en… … Wikipédia en Français
ÉLASTICITÉ — La théorie de l’élasticité est la théorie des petites déformations continues et réversibles des milieux isotropes élastiques. Elle donne, en principe et moyennant certaines hypothèses, la solution théorique complète des problèmes posés en… … Encyclopédie Universelle
Glossaire de la mécanique — Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A Accélération : . Accouplement : . Acoustique … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Coefficients de lamé