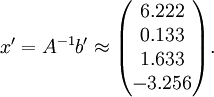Coefficient de conditionnement

Coefficient de conditionnement

Conditionnement (analyse numérique)

Page d'aide sur l'homonymie Pour les articles homonymes, voir Conditionnement.

En général, les données d'un problème numérique dépendent de mesures expérimentales et sont donc entachées d'erreur.

Le conditionnement mesure la dépendance de la solution d'un problème numérique par rapport aux données du problèmes, ceci afin de contrôler la validité d'une solution calculée par rapport à ces données. Il s'agit le plus souvent d'une quantité numérique, parfois appelée nombre de conditionnement.

De façon plus générale, on peut dire le nombre de conditionnement associé à un problème est une mesure de la difficulté de calcul numérique du problème. Un problème possédant un nombre de conditionnement bas est dit bien conditionné et un problème possédant un nombre de conditionnement élevé est dit mal conditionné.

Conditionnement d'un système linéaire

Pour un système linéaire "Ax = b", où les données sont la matrice A et le vecteur second membre b, le conditionnement donne une borne de l'erreur relative commise sur la solution x lorsque les données A,b sont perturbées. Il peut s'avérer que cette borne soit très grande, de sorte que l'erreur qui pourrait en découler rende la solution numérique inexploitable.


S'étant donné une norme vectorielle, notant ||\cdot|| la norme matricielle subordonnée correspondante, le nombre de conditionnement d'une matrice inversible est défini par la formule :

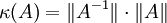\kappa(A) = \Vert A^{-1}\Vert \cdot \Vert A\Vert.

Alors, le calcul effectif de l'inversion du système Ax = b, où la matrice A est connue avec précision et où la valeur second membre b est entachée d'une erreur Δb produira une erreur relative théorique (dans la mesure où on suppose que les calculs sont faits avec une précision infinie) sur la solution x majorée par

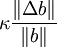\kappa \frac{\Vert \Delta b\Vert}{\Vert b\Vert}.

Un exemple de matrice mal conditionnée

Soit la matrice

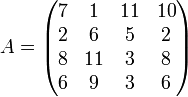A=\begin{pmatrix} 7 &1 & 11& 10\\ 2 & 6 & 5 & 2\\ 8 & 11 & 3 & 8\\ 6 & 9& 3&6\\ \end{pmatrix},

et le vecteur

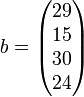b=\begin{pmatrix} 29\\ 15\\ 30\\ 24\\ \end{pmatrix}.

La résolution du système Ax = b donne

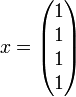x=\begin{pmatrix} 1\\ 1\\ 1\\ 1\\ \end{pmatrix}.


Si on substitue au second membre b le second membre perturbé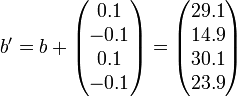

b'=b+\begin{pmatrix} 0.1\\ -0.1\\ 0.1\\ -0.1\\ \end{pmatrix}=\begin{pmatrix} 29.1\\ 14.9\\ 30.1\\ 23.9\\ \end{pmatrix},

la solution x' correspondante sera

x'=A^{-1}b'\approx \begin{pmatrix} 6.222\\ 0.133\\ 1.633\\ -3.256\\ \end{pmatrix}.

Les erreurs relatives de b et x sont respectivement de 0.004 et 3.4108 ce qui représente une multiplication par environ 860 de l'erreur relative. Ce nombre est du même ordre que le conditionnement de la matrice A qui est de 1425.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Conditionnement (analyse num%C3%A9rique) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Coefficient de conditionnement de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Matrice De Hilbert — En algèbre linéaire, la matrice de Hilbert est une matrice carrée de terme général Bij = 1 / (i + j − 1). Elle est nommée ainsi en hommage au mathématicien David Hilbert. Les matrices de Hilbert servent d exemples classiques de matrices mal… …   Wikipédia en Français

  • Matrice de Hilbert — En algèbre linéaire, la matrice de Hilbert est une matrice carrée de terme général Bij = 1 / (i + j − 1). Elle est nommée ainsi en hommage au mathématicien David Hilbert. Les matrices de Hilbert servent d exemples classiques de matrices mal… …   Wikipédia en Français

  • Matrice de hilbert — En algèbre linéaire, la matrice de Hilbert est une matrice carrée de terme général Bij = 1 / (i + j − 1). Elle est nommée ainsi en hommage au mathématicien David Hilbert. Les matrices de Hilbert servent d exemples classiques de matrices mal… …   Wikipédia en Français

  • Variable régionalisée — La VR comme phénomène physique : topographie de la ville de Binche …   Wikipédia en Français

  • VERRE — Les verres constituent un ensemble extrêmement varié de produits dont les propriétés sont innombrables. Celles ci dépendent fortement des traitements subis, thermiques notamment. Leur mise au point résulte aujourd’hui des progrès des… …   Encyclopédie Universelle

  • ÉNERGIES RENOUVELABLES — Les énergies renouvelables utilisent des sources inépuisables d’énergies d’origine naturelle: rayonnement solaire, vents, cycles de l’eau et du carbone dans la biosphère, flux de chaleur interne de la Terre, effet de l’attraction lunaire et… …   Encyclopédie Universelle

  • Ampoule (Récipient) — Pour les articles homonymes, voir Ampoule. Certains médicaments injectables (vaccins, sérums, ...) ou buvables sont contenus dans des ampoules en verre dont on casse une extrémité (comme celles de la photo). Dans d autres cas l ampoule a une… …   Wikipédia en Français

  • Ampoule (recipient) — Ampoule (récipient) Pour les articles homonymes, voir Ampoule. Certains médicaments injectables (vaccins, sérums, ...) ou buvables sont contenus dans des ampoules en verre dont on casse une extrémité (comme celles de la photo). Dans d autres cas… …   Wikipédia en Français

  • Ampoule (récipient) — Pour les articles homonymes, voir Ampoule. Certains médicaments injectables (vaccins, sérums, ...) ou buvables sont contenus dans des ampoules en verre dont on casse une extrémité (comme celles de la photo). Dans d autres cas l ampoule a une… …   Wikipédia en Français

  • Ampoule pharmaceutique — Ampoule (récipient) Pour les articles homonymes, voir Ampoule. Certains médicaments injectables (vaccins, sérums, ...) ou buvables sont contenus dans des ampoules en verre dont on casse une extrémité (comme celles de la photo). Dans d autres cas… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”