Chiffres significatifs

Chiffres significatifs

Chiffre significatif

Dans une mesure physique, le nombre de chiffres significatifs détermine la précision de la mesure. Il s'agit des chiffres connus avec certitude plus le premier chiffre incertain.

Par exemple: 1234 a 4 chiffres significatifs. Le premier chiffre incertain est le 4.

Cas du 0

  • Lorsque le 0 est placé à gauche, il n'est pas significatif:

0,8 a 1 chiffre significatif
0,0052 a 2 chiffres significatifs
031 a 2 chiffres significatifs

  • Lorsque 0 est placé entre deux chiffres significatifs non nuls, il est significatif:

1203 a 4 chiffres significatifs
12,03 a 4 chiffres significatifs
120,4 a 4 chiffres significatifs

  • Lorsque le 0 est placé à droite, mais après la virgule, il est significatif:

1,200 a 4 chiffres significatifs
0,0520 a 3 chiffres significatifs

  • Le cas des nombres entiers tels: 400, 1000, 10... est ambigu.

Par exemple 400 peut s'écrire de diverses façons:
400 avec 3 chiffres significatifs
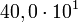40,0\cdot 10^{1} avec 3 chiffres significatifs
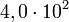4,0\cdot 10^{2} avec 2 chiffres significatifs
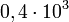0,4\cdot 10^{3} avec 1 seul chiffre significatif

Selon la façon dont il est écrit, le nombre de chiffres significatifs varie. Il est donc préférable d'écrire de tels nombres en notation scientifique.

En notation scientifique, tous les chiffres de la mantisse sont significatifs.

Convention

On rencontre fréquemment dans les tables des valeurs telles:

12,43

Avec 4 chiffres significatifs.

Par convention il s'agit d'une valeur abrégée pour:

12,43 +/- 0,01

Sommaire

Chiffres significatifs et opérations

Lors d'un calcul, les données sont parfois fournies avec des nombres de chiffres significatifs différents. Le résultat du calcul doit alors être exprimé avec le nombre de chiffres significatifs de la donnée qui en possède le moins.

Addition et soustraction

Après une addition ou une soustraction, le résultat ne doit pas avoir plus de décimales que le nombre qui en comporte le moins.

Exemple 1

On calcule la masse molaire du thiosulfate de sodium pentahydraté Na2S2O3 , 5H2O :

M(Na) = 23,0 g.mol−1
M(O) = 16,0 g.mol−1
M(S) = 32,05 g.mol−1
M(H) = 1,008 g.mol−1
M(Na2S2O3 , 5H2O) = 248,2 g.mol−1 (M(Na) et M(O) n'ont qu'une décimale)

Exemple 2

Simplifier : Périmètre du rectangle: L= 143 cm (donc 3 chiffres significatifs et pas de décimale) et l= 5,7 cm (donc 2 chiffres significatifs et une décimale)

P= 2x(5,7+143) P= 2x148.7 P= 297.4

Mais 143 n'ayant pas de décimale, le périmètre ne doit pas en avoir non plus donc: P= 297 cm

Multiplication et division

Après une multiplication ou une division, le résultat ne doit pas avoir plus de chiffres significatifs que la valeur la moins précise.

Exemple

On dissout une masse m = 6,17 g de thiosulfate de sodium pentahydraté M = 248,2 g.mol−1 dans un volume V = 150,0 mL de solution, la concentration molaire apportée est :

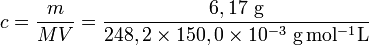
c = \frac{m}{MV} = \frac{6,17 \rm~g}{248,2\times 150,0\times 10^{-3}\rm~g\,mol^{-1}L}

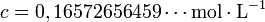c = 0,16572656459\cdots \mathrm{ mol}\cdot \mathrm{L}^{-1} \, résultat brut, incorrect.

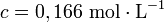c = 0,166 ~\mathrm{ mol}\cdot\mathrm{L}^{-1}\, résultat correct avec 3 chiffres significatifs

les logarithmes

Les logarithmes ont le même nombre de chiffres significatifs que leur argument. Cette règle amène à des subtilités avec le logarithme décimal.

les nombres: 4,2 102 et 4,2 103 sont tous deux donnés avec 2 chiffres significatifs.

Leurs logarithmes décimaux donnent respectivement:

2,6232.... 3,6232...

On constate donc que le nombre avant la virgule n'est que la valeur de l'exposant. Cette valeur ne servant qu'à positionner la virgule, elle n'est pas elle-même un chiffre significatif. Par conséquent le logarithme de nos deux nombres avec 2 chiffres significatifs doit s'écrire:

2,62

Articles connexes

Notes et références

Ce document provient de « Chiffre significatif ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Chiffres significatifs de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Chiffres précis — Erreur d approximation En analyse numérique, une branche des mathématiques, l erreur d approximation de certaines données est la différence entre une valeur exacte et une certaine valeur approchée ou approximation de celle ci. Une erreur d… …   Wikipédia en Français

  • Chiffre Significatif — Dans une mesure physique, le nombre de chiffres significatifs détermine la précision de la mesure. Il s agit des chiffres connus avec certitude plus le premier chiffre incertain. Par exemple: 1234 a 4 chiffres significatifs. Le premier chiffre… …   Wikipédia en Français

  • Chiffre significatif — Dans une mesure physique, le nombre de chiffres significatifs indique la précision de la mesure. Il s agit des chiffres connus avec certitude plus le premier chiffre incertain. La précision (ou l incertitude) avec laquelle on connait la valeur d… …   Wikipédia en Français

  • Vitesse de convergence des suites — En analyse numérique, qui est une branche des mathématiques, on peut classer les suites convergentes en fonction de leur vitesse de convergence vers leur point limite. C est une manière d apprécier l efficacité des algorithmes qui les génèrent.… …   Wikipédia en Français

  • significatif — significatif, ive [ siɲifikatif, iv ] adj. • fin XVe; bas lat. significativus 1 ♦ Qui signifie nettement, exprime clairement qqch. ⇒ éloquent, expressif. « Le plus significatif des symboles qu imaginèrent jadis les Indiens pour figurer [...] Dieu …   Encyclopédie Universelle

  • Pi — Pour les articles homonymes, voir Pi (homonymie). Si le diamètre du cercle est 1, sa circonférence est π. Pi[1 …   Wikipédia en Français

  • Peak-oil — Pic pétrolier Un pic pétrolier désigne le sommet de la courbe qui caractérise la production pétrolière d un puits ou d un champ pétrolier ; par extension le « pic pétrolier mondial » (abrégé en Peak Oil en anglais) désigne le… …   Wikipédia en Français

  • Peak oil — Pic pétrolier Un pic pétrolier désigne le sommet de la courbe qui caractérise la production pétrolière d un puits ou d un champ pétrolier ; par extension le « pic pétrolier mondial » (abrégé en Peak Oil en anglais) désigne le… …   Wikipédia en Français

  • Pic de pétrole — Pic pétrolier Un pic pétrolier désigne le sommet de la courbe qui caractérise la production pétrolière d un puits ou d un champ pétrolier ; par extension le « pic pétrolier mondial » (abrégé en Peak Oil en anglais) désigne le… …   Wikipédia en Français

  • Pic du pétrole — Pic pétrolier Un pic pétrolier désigne le sommet de la courbe qui caractérise la production pétrolière d un puits ou d un champ pétrolier ; par extension le « pic pétrolier mondial » (abrégé en Peak Oil en anglais) désigne le… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”