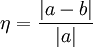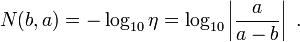- Chiffres précis
-
Erreur d'approximation
En analyse numérique, une branche des mathématiques, l'erreur d'approximation de certaines données est la différence entre une valeur exacte et une certaine valeur approchée ou approximation de celle-ci. Une erreur d'approximation peut se produire
- lorsque la mesure des données n'est pas précise (en raison des instruments) ;
- ou lors de l'emploi de valeurs approchées au lieu des valeurs exactes (par exemple, 3,14 au lieu de π).
On distingue généralement l'erreur relative et l'erreur absolue. La stabilité numérique d'un algorithme, en analyse numérique, indique comment l'erreur est propagée par l'algorithme.
Définition
Étant données une valeur a et une valeur approchée b de a, l'erreur absolue est par définition le nombre
- ε = | a − b |
et quand a est non nul, l'erreur relative est le nombre
où les barres verticales désignent la valeur absolue.
On définit également le nombre de chiffres précis comme
Cette quantité mesure la précision, et donne une estimation du nombre de chiffres significatifs que l'approximation b a en commun avec la valeur exacte a. Cependant, cette estimation peut être très différente du nombre de chiffres qui coïncident, ainsi 1.000 possède plus de chiffres précis que 0.990, lorsque les deux sont considérées comme approximations de 0.999, car l'erreur relative est environ 0.001 pour la première, soit 3 chiffres précis au sens de la définition précédente, alors que l'erreur relative 9 fois plus élevée de la deuxième correspond à presque 1 chiffre précis de moins.
Exemple
Développons les exemples de
- b = 1.234 comme approximation de a = 1.2345.
- b = 3.1415 comme approximation de a = π ≈ 3.14159...
- b = 3.1416 comme approximation de a = π ≈ 3.14159... (Commentaire ?)
Voir aussi
Catégorie : Analyse numérique
Wikimedia Foundation. 2010.