- Chiffre De Playfair
-
Chiffre de Playfair
 Le Chiffre de Playfair, fut inventé par Charles Wheatstone, qui le décrit pour la première fois en 1854.
Le Chiffre de Playfair, fut inventé par Charles Wheatstone, qui le décrit pour la première fois en 1854.
Le Chiffre de Playfair ou Carré de Playfair est une méthode manuelle de chiffrement symétrique qui fut la première technique utilisable en pratique de chiffrement par substitution polygrammique. Il fut imaginé en 1854 par Charles Wheatstone, mais porte le nom de Lord Playfair qui popularisa son utilisation.
Il consiste à chiffrer des paires de lettres (des digrammes), plutôt que des lettres seules comme dans les chiffrements par subsitutions poly-alphabétiques tels que le chiffre de Vigenère, plus répandus à l'époque. Ce chiffrement est significativement plus dur à casser car les attaques par analyse fréquentielle habituellement utilisées sur les chiffrements par substitutions simples sont peu efficaces sur lui. L'analyse de fréquence des digrammes reste toujours possible, mais appliquée à six cents[1] digrammes possibles au lieu des 26 lettres de l'alphabet, elle est considérablement plus difficile et exige un texte chiffré beaucoup plus long pour espérer être efficace.
Sommaire
Historique
La première description écrite de ce chiffrement fut trouvée dans un document signé par Wheatstone le 26 mars 1854. Il fut refusé par le British Foreign Office qui le trouvait d'une trop grande complexité. Quand Wheatstone proposa de montrer qu'il pouvait être maitrisé par les trois quarts des garçons de l'école voisine en moins de 15 minutes, le Sous-Secrétaire du Foreign Office aurait répondu : « C'est très possible, mais vous n'arriverez pas à le faire apprendre à des spécialistes ».
Il a été utilisé par les forces britanniques durant la Seconde Guerre des Boers et la Première Guerre mondiale et aussi par les Australiens pendant la Seconde Guerre mondiale.
La première solution fut décrite en 1914 dans un essai de 19 pages du Lieutenant Joseph O. Mauborgne.
Méthode de chiffrement
Le chiffre de Playfair utilise un tableau de 5x5 lettres, contenant un mot clé ou une phrase. La mémorisation du mot clé et de 4 règles faciles à suivre suffisait pour utiliser ce chiffrement.
Pour construire le tableau, on devait d'abord le remplir avec les lettres du mot clé (en ignorant les doublons), puis le compléter avec les autres lettres de l'alphabet dans l'ordre (soit en omettant la lettre Q, soit en occupant une même case pour les lettres I et J suivant les versions). Le mot clé peut être écrit en ligne, en colonne ou même en spirale.
Pour chiffrer un message, il faut prendre les lettres 2 par 2 et appliquer les règles suivantes en fonction de la position des lettres dans la table :
- si les 2 lettres sont identiques (ou s'il n'en reste qu'une) mettre un 'X' après la première lettre. Chiffrer la nouvelle paire ainsi constituée et continuer avec la suivante. Dans certaines variantes, on utilise 'Q' au lieu du 'X', mais n'importe quelle lettre peut faire l'affaire,
- si les lettres se trouvent sur la même ligne de la table, il faut les remplacer par celles se trouvant immédiatement à leur droite (en bouclant sur la gauche si le bord est atteint),
- si les lettres apparaissent sur la même colonne, les remplacer par celles qui sont juste en dessous (en bouclant par le haut si le bas de la table est atteint),
- sinon, remplacer les lettres par celles se trouvant sur la même ligne, mais dans le coin opposé du rectangle défini par la paire originale.
Pour chiffrer le digramme 'OR' par exemple, trois configurations peuvent se présenter dans le tableau :
1) sur la même ligne
* * * * * * O Y R Z * * * * * * * * * * * * * * *
alors, OR → YZ
2) sur la même colonne
* * O * * * * B * * * * * * * * * R * * * * Y * *
alors, OR → BY
3) forment un rectangle
Z * * O * * * * * * * * * * * R * * X * * * * * *
alors, OR → ZX
Pour déchiffrer, utiliser la méthode inverse en ignorant les 'X' ou les 'Q' qui n'ont pas leur place dans le message final, c'est-à-dire en prenant les lettres à gauche dans le cas d'une même ligne, vers le haut dans le cas d'une même colonne, et toujours les coins dans le cas d'un rectangle.
Exemple
En supposant que la clé soit "exemple playfair", le tableau doit alors être rempli comme suit :
E X M P L A Y F I R B C D G H J K N O Q S T U V Z
Chiffrement du message "Cache l'or dans la souche de l'arbre" :
CA CH EL OR DA NS LA SO UC HE DE LA RB RE
soit
BY DB XE QI BF JU ER VJ TD BL BM ER AH AL
Cryptanalyse
Comme la plupart des chiffrements anciens, le Chiffre de Playfair peut facilement être cassé si l'on dispose de suffisamment d'échantillons. Obtenir la clé est relativement rapide si l'on a connaissance à la fois du texte chiffré et du texte clair (attaque à texte clair connu).
Lien externe
Notes et références
- ↑ c'est à savoir : 600 =
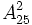
- Portail de la cryptologie
Catégorie : Algorithme de cryptographie symétrique
Wikimedia Foundation. 2010.

