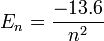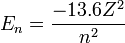Case Quantique

Case Quantique

Case quantique

En physique, en mécanique quantique, dans le modèle de Bohr, les cases quantiques sont les places dans les orbitales atomiques qui peuvent être occupées par un électron, ou par une paire d'électrons de spin complémentaires.

Nombres quantiques

Le nuage électronique de chaque atome peut être défini par quatre nombres dits « quantiques », puisqu'ils ne prennent que certaines valeurs quantifiées :

  • n : nombre quantique « principal » qui peut prendre toutes les valeurs entières égales ou supérieures à 1 soit 1, 2, 3, 4… Il définit en grande partie l'énergie de l'électron ainsi que la taille de l'orbitale qui augmente à mesure que n augmente.
  • l : nombre quantique « secondaire » qui peut prendre toutes les valeurs entières comprises entre 0 et n-1. Cela signifie par exemple, dans le cas où n = 2, que l peut être égal à 0 ou à 1. Ce nombre définit principalement la forme de l'orbitale. Avec l = 0 la forme est sphérique, avec 1 une forme bilobée, l = 2 forme ayant 4 lobes, l = 3 huit lobes et ainsi de suite. Il aide aussi à déterminer l'énergie de l'électron et sa distance moyenne au noyau.
  • ml (ou m) : nombre quantique « magnétique » qui peut prendre toutes les valeurs entières comprises entre -l et +l, il définit l'orientation de l'orbitale décrite par l'électron. Plus l est élevé, plus il y a d'orientations différentes possibles pour cette orbitale.
  • ms (ou s) : nombre quantique de « spin » qui représente le spin de l'électron, à savoir +1/2 ou -1/2. Il est indépendant des autres nombres quantiques. On peut classiquement l'interpréter comme un « moment cinétique intrinsèque. » Il représente en réalité plutôt la symétrie du fermion.

En fonction des nombres quantiques auxquels on a accès, on peut définir plus ou moins précisément une partie de ce nuage :

  • Si les 4 nombres quantiques sont connus, l'état permis de l'électron est défini ;
  • Si les 3 premiers nombres quantiques sont connus, alors l'orbitale de l'électron est définie.

Pour désigner plus facilement une orbitale ou un état de l'électron, une notation symbolique est utilisée. Le nombre principal n est désigné par un chiffre, l par une lettre et la valeur de m est en indice. Le spin est noté par un tiret pour la valeur -1/2, et rien pour la valeur +1/2.

  • « s » pour l = 0 (sharp)
  • « p » pour l = 1 (principal)
  • « d » pour l = 2 (diffuse)
  • « f » pour l = 3 (fundamental)
  • …

Par exemple :

  • 4f − 2 signifie n = 4, l = 3, ml = -2, ms = +1/2 ;
  • 2p + 1 signifie n = 2, l = 1, ml' = +1, ms = +1/2.

Influence du numéro atomique sur l'énergie

Plus l'électron occupe une orbitale basse, comme l'orbitale 1s, fondamentale, plus l'énergie qu'il contient est faible. La taille d'une orbitale dépend beaucoup de son énergie.

Pour l'hydrogène, l'énergie correspond seulement au nombre quantique n. Pour cet atome, et seulement lui, la formule de l'énergie fournie par la mécanique quantique est exactement la même que celle du modèle de Bohr, soit (en eV) :

E_n = \frac{-13.6}{n^2}

La valeur -13,6 eV, qui correspond à l'état fondamental de l'hydrogène, est la constante de Rydberg. On peut étendre ce modèle aux ions dits « hydrogénoïde » (ne possédant qu'un seul électron) :

E_n = \frac{-13.6 Z^2}{n^2}

Pour les autres atomes, l'énergie des électrons dépend de n et de l (pas de ml ni de ms). La règle de Klechkowski est utilisée pour la déterminer - mais il existe de nombreuses exceptions. En réalité, elle permet de savoir quel électron a plus d'énergie que les précédents. Pour l'hydrogène, le niveau d'énergie 2s = 2p mais pour l'hélium 2s < 2p à cause de l.

Plus un atome possède de protons, plus les électrons sont difficiles à « enlever » c'est-à-dire moins ils possèdent d'énergie. Ainsi le niveau d'énergie de l'hydrogène 1s est très supérieur au niveau d'énergie 1s de l'hélium, tandis qu'avec les mêmes atomes, le niveau 2s est à peu près au même niveau (en réalité, un peu plus bas). Plus il y a de protons, plus les tailles des orbitales diminuent.

Configuration électronique à l'état fondamental

Le principe d'exclusion de Pauli énonce que dans un même atome, deux électrons ne peuvent posséder leurs quatre nombres quantiques identiques ; n, l et ml définissent une « case quantique » (les deux valeurs possibles de ms définissent une orientation de l'électron). Chaque case quantique peut contenir 0, 1 électron (de spin up) ou 2 électrons (de spins opposés).

C'est la première règle de l’ « Aufbau Prinzip » : l'atomistique.

  • Portail de la physique Portail de la physique
  • Portail de la chimie Portail de la chimie
Ce document provient de « Case quantique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Case Quantique de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Case quantique — En physique, en mécanique quantique, dans le modèle de Bohr, les cases quantiques sont les places dans les orbitales atomiques qui peuvent être occupées par un électron, ou par une paire d électrons de spin complémentaires. Nombres quantiques Le… …   Wikipédia en Français

  • Nombre Quantique — Un nombre quantique est, en mécanique quantique, un élément d un jeu de nombres permettant de définir l état quantique complet d un système. Chaque nombre quantique définit la valeur d une quantité conservée dans la dynamique d un système… …   Wikipédia en Français

  • Nombre quantique — Un nombre quantique est, en mécanique quantique, un élément d un jeu de nombres permettant de définir l état quantique complet d un système. Chaque nombre quantique définit la valeur d une quantité conservée dans la dynamique d un système… …   Wikipédia en Français

  • Nombre Quantique Secondaire — En physique, en mécanique quantique, dans le modèle de Bohr, le nombre quantique secondaire, aussi appelé nombre quantique azimutal est le deuxième des quatre nombres qui définissent l état quantique d un électron. On peut considérer qu il… …   Wikipédia en Français

  • Nombre quantique azimutal — Nombre quantique secondaire En physique, en mécanique quantique, dans le modèle de Bohr, le nombre quantique secondaire, aussi appelé nombre quantique azimutal est le deuxième des quatre nombres qui définissent l état quantique d un électron. On… …   Wikipédia en Français

  • Nombre quantique secondaire — En physique, en mécanique quantique, dans le modèle de Bohr, le nombre quantique secondaire, aussi appelé nombre quantique azimutal est le deuxième des quatre nombres qui définissent l état quantique d un électron. On peut considérer qu il… …   Wikipédia en Français

  • Nombre Quantique Magnétique — En physique, en mécanique quantique, dans le modèle de Bohr, le nombre quantique magnétique, aussi appelé nombre quantique tertiaire, soit le troisième nombre quantique, symbolisé par ml détermine l orientation spatiale d une orbitale. Le nombre… …   Wikipédia en Français

  • Nombre quantique magnetique — Nombre quantique magnétique En physique, en mécanique quantique, dans le modèle de Bohr, le nombre quantique magnétique, aussi appelé nombre quantique tertiaire, soit le troisième nombre quantique, symbolisé par ml détermine l orientation… …   Wikipédia en Français

  • Nombre quantique tertiaire — Nombre quantique magnétique En physique, en mécanique quantique, dans le modèle de Bohr, le nombre quantique magnétique, aussi appelé nombre quantique tertiaire, soit le troisième nombre quantique, symbolisé par ml détermine l orientation… …   Wikipédia en Français

  • Nombre quantique magnétique — En physique, en mécanique quantique, dans le modèle de Bohr, le nombre quantique magnétique, aussi appelé nombre quantique tertiaire, soit le troisième nombre quantique, symbolisé par ml détermine l orientation spatiale d une orbitale. Le nombre… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”