- Capital asset pricing model
-
Modèle d'évaluation des actifs financiers
 Pour les articles homonymes, voir CAPM.
Pour les articles homonymes, voir CAPM.Le Modèle d'évaluation des actifs financiers (MEDAF), traduction approximative[1] de l'anglais Capital Asset Pricing Model (CAPM) fournit une estimation de valeur théorique d'un actif financier. Cette théorie prend en compte l'aversion naturelle des investisseurs pour le risque (plus précisément, ils cherchent à maximiser leur profit pour un risque donné, ou à profit donné veulent minimiser le risque pris). Historiquement, ce modèle a été invalidé : sur la période de 1963 à 2006 aux Etats-Unis, les actions aux coefficients bétas les plus faibles ont eu le meilleur retour sur investissement, alors que celles a béta elevé ont eu les rendements les plus faibles - en contradiction complète avec le modèle [2]!
Sommaire
Hypothèses
Le MEDAF postule les hypothèses théoriques suivantes :
- Il n'y a pas de coûts de transaction (pas de commission, et pas de marge bid-ask).
- Un investisseur peut acheter ou vendre à découvert n'importe quelle action sans que cela ait une incidence sur le prix de l'action
- Il n'y a pas de taxes (notamment, il est le même pour les plus-values et les dividendes)
- Les investisseurs n'aiment pas le risque
- Les investisseurs ont le même horizon temporel
- Tous les investisseurs ont un portofolio de Markowitz car ils ne considèrent chaque action que sous son aspect moyenne-variance
- Les investisseurs contrôlent le risque par la diversification
- Tous les actifs, y compris le capital humain, peuvent être achetés et vendus librement sur le marché.
- Les investisseurs peuvent prêter ou emprunter de l'argent au taux sans risque.
Il faut remarquer que la plupart de ses hypothèses ne sont pas verifiées en réalité, en particulier la # 2 et # 6 :
- Toute transaction d'une certaine taille a un effet sur le prix d'une action
- Peu d'investisseurs ont un portofolio de Markowitz (l'inventeur de ce portofolio, Harry Markowitz lui même ne l'utilise pas [3]; George Akerlof non plus[4])
Harry Markowitz a écrit dans un article de 2005 du Financial Analysts Journal que si l'on modifie l'hypothèse # 9 alors les conclusions de son modèle sont modifiées drastiquement.[5] En effet, l'hypothèse # 9 stipule qu'un investisseur peut emprunter de l'argent sans limite de taille, ce qu'aucune banque (heureusement !) n'autorise aujourd'hui.
Définition
Le Medaf ou Capital Asset Pricing Model explique la réalisation de l'équilibre du marché par l'offre et la demande pour chaque titre. Il permet de déterminer le rendement d'un actif risqué par son risque systématique.
Les transactions cesseront lorsque les opérateurs auront un portefeuille identique
La formule est une fonction :
- de la mesure du risque systématique de l'actif, c'est-à-dire au risque non diversifiable (l'investisseur diversifiera son portefeuille directement sur le marché), noté
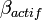 (coefficient bêta de l'actif) ;
(coefficient bêta de l'actif) ; - de la rentabilité espérée sur le marché, notée
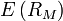 ;
; - du taux d'intérêt sans risque (généralement des emprunts d'État), noté
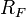 .
.
![E(R_{actif}) = R_F + \beta_{actif}\cdot [E(R_M) - R_F]](/pictures/frwiki/99/cc575bba3d4b39504da4dc545d6440cc.png)
![[E(R_M) - R_F] \,](/pictures/frwiki/53/5156408ee615810bf967ce0851831885.png) représente la prime de risque du marché, c'est-à-dire le surplus de rentabilité exigé par les investisseurs lorsque ces derniers placent leur argent sur le marché, plutôt que dans un actif sans risque.
représente la prime de risque du marché, c'est-à-dire le surplus de rentabilité exigé par les investisseurs lorsque ces derniers placent leur argent sur le marché, plutôt que dans un actif sans risque.Le
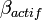 est la volatilité de la rentabilité de l'actif considéré rapportée à celle du marché. Mathématiquement parlant, elle correspond au rapport entre la covariance de la rentabilité de l'actif et de la rentabilité du marché et la variance du risque du marché.
est la volatilité de la rentabilité de l'actif considéré rapportée à celle du marché. Mathématiquement parlant, elle correspond au rapport entre la covariance de la rentabilité de l'actif et de la rentabilité du marché et la variance du risque du marché.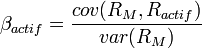
Dans le modèle MEDAF (ou CAPM), on peut montrer que ce coefficient correspond à l'élasticité du cours du titre par rapport à l'indice boursier représentant le marché.
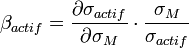
où
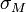 représente le risque du marché (l'écart-type de
représente le risque du marché (l'écart-type de 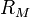 ) et
) et 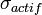 le risque de l'actif (l'écart-type de la rentabilité attendue de l'actif). Ainsi, un actif représentant le marché aura un
le risque de l'actif (l'écart-type de la rentabilité attendue de l'actif). Ainsi, un actif représentant le marché aura un 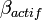 égal à 1. Pour un actif sans risque, il sera égal à 0.
égal à 1. Pour un actif sans risque, il sera égal à 0.Une théorie invalidée
Le modèle de prix théorique MEDAF a été invalidé par la pratique. Le modèle prévoit une relation linéaire entre le rendement d'un actif financier et son béta. En réalité, c'est l'inverse qui a été vérifié. Jeremy Grantham, analyste chez GMO, a analysé la relation entre le beta et le rendement sur les 600 actions aux capitalisations boursières les plus importantes du marché boursier américain : les actions aux coefficients bétas les plus faibles ont eu le meilleur retour sur investissement, alors que celles a béta elevé ont eu les rendements les plus faibles - en contradiction complète avec le modèle ![6]. Cette relation a aussi été verifié par James Montier, analyste à la Société Générale pour les actions européenes de 1986 à 2006.[7].
Le modèle a aussi été invalidé en 2004 par une étude de Eugène Fama et Kenneth French publiée en 2004[8]. Ils y déclarent que : "Malheureusement, à cause de la simplicité de ce modèle, la vérification empirique de ce modèle est pauvre - tellement pauvre qu'elle invalide son utilisation."
Une théorie améliorée ?
Eugène Fama et Kenneth French ont publié en 1992 une étude célèbre[9] remettant en cause le CAPM, surnommée depuis le "Beta is dead" paper (« l' article annonçant la mort de Bêta »). Elle attribuait l'essentiel des variations de prix non au bêta mais à deux autres coefficients de marché :
- le Price earning ratio (PER)
- et le ratio capitalisation boursière sur actif net comptable (Price to book value (PBV), appelé aussi, en prenant le ratio inverse, Book to market).
Un modèle devenu populaire en est dérivé, le Three-factor model.
Un modèle allant dans ce sens mais encore plus étendu est l'APT (Arbitrage Pricing Theory) de Ross qui accepte des bêtas multiples dont chacun correspond à un facteur quantifiable particulier.
Enfin, les recherches en finance comportementale ont introduit d'autres élements, par exemple les sur-réactions et sous-réactions du marché aux informations.
Voir aussi
Notes
- ↑ Pricing signifie formation du prix et non pas évaluation. D'ailleurs certains auteurs préfèrent la traduction "Modèle d'équilibre des actifs financiers"
- ↑ [1] Voir, en particulier, page 20
- ↑ Lorsqu'interrogé sur la façon qu'il placait ses fonds :"Mon intention est de ne pas avoir de regrets dans le futur. J'investis 50% dans des obligations, 50% dans des actions, Behavorial Investing, James Montier, Wiley Finance, 2007, page 431
- ↑ George Akerlof place une part importante de son argent dans des fonds mutuels, Behavorial Investing, James Montier, Wiley Finance, 2007, page 431
- ↑ Article de Markowitz dans FAJ
- ↑ [2] Voir, en particulier, page 20
- ↑ James Montier, Behavorial Investing, Wiley Finance, 2007, page 430
- ↑ [3] The Capital Asset Pricing Model: Theory and Evidence, Journal of Economic Perspectives—Volume 18, Numéro 3—Été 2004—Pages 25–46
- ↑ Eugène Fama et Kenneth French, The cross-section of expected stock returns, Journal of finance, Juin 1992.
- Portail de l’économie
- Portail de la finance
Catégorie : Évaluation d'actif
Wikimedia Foundation. 2010.
