- Bâton d'Ishango
-
Os d'Ishango
L’os d'Ishango, également appelé bâton d'Ishango, est un vestige archéologique daté de près de 23 000 ans avant notre ère. Selon certains auteurs, il pourrait s'agir de la plus ancienne attestation de la pratique de l'arithmétique dans l'histoire de l'humanité. Cette thèse est cependant controversée.
Sommaire
Découverte et principales caractéristiques
L'archéologue belge Jean de Heinzelin de Braucourt mit au jour cet ossement en 1950 au bord du lac Édouard dans la région d'Ishango en République démocratique du Congo, près de l'Ouganda ; l'ossement est exposé au Muséum des Sciences naturelles de Bruxelles en Belgique[1].
Il s'agit d'un os de 10,2 cm, provenant d'un animal non identifié, découvert dans des couches de cendres volcaniques. Un fragment de quartz est enchâssé à son sommet. Il porte plusieurs incisions, organisées en groupe sur trois colonnes. Bien qu'il n'existe que des présomptions quant à sa signification arithmétique, l’os fait l’objet de nombreuses interprétations.
Le problème du déchiffrement
 Colonne a
Colonne a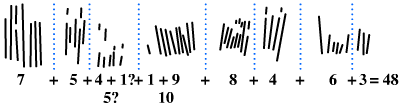 Colonne b
Colonne b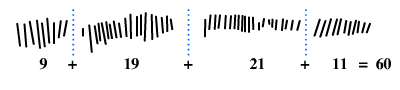 Colonne c
Colonne cLes entailles présentes sur l'os d'Ishango furent interprétées, selon les auteurs, comme une calculette préhistorique, un calendrier lunaire ou un code barre préhistorique.
Jeux arithmétiques ?
Dans les années 1950, Jean de Heinzelin fut le premier à considérer cet os comme un vestige présentant un intérêt pour l'histoire des mathématiques. Il l'assimila à un jeu d'arithmétique et donna un ordre arbitraire aux différentes colonnes, soit la première (b), la seconde (c) et la troisième (a) en suivant les notations du schéma ci-dessous.
L'inventeur nota que la colonne (c) est compatible avec un système de numération de base 10, du fait que les entailles y sont groupées comme 20 + 1, 20 - 1, 10 + 1, 10 - 1. Il reconnut également, en colonne (a), l'écriture dans l'ordre des nombres premiers compris entre 10 et 20, soit 11, 13, 17 et 19. Enfin, la colonne (b) semble illustrer la méthode de duplication multiplication par 2 utilisée en une période plus proche de nous dans la multiplication égyptienne, soit 3 x 2 = 6, 4 x 2 = 8 et 5 x 2 = 10.
Suite à ses observations, J. de Heinzelin admet de fait que les « paléo-mathématiciens » d'Ishango avaient la connaissance des nombres premiers. De plus certains continuateurs des travaux de J. de Heinzelin admettent que, dans la mesure où ces mathématiciens avaient la connaissance pratique des nombres premiers, ils devaient tout aussi naturellement connaître les deux théorèmes d'arithmétique élémentaires suivants :
Théorème 1 : Pour tout entier naturel n, 2(n + 1) = 2n + 2
Théorème 2 : Pour tout entier naturel n, 3n = 2n + n
Plus que comme un jeu mathématique, l'os d'Ishango semble se présenter comme un document crypté faisant appel à l'arithmétique et fondé sur les nombres premiers et les duplications.
Calendrier lunaire ?
Dans les années 1970, le journaliste scientifique Alexander Marshack nota que la somme de tous les nombres donnait 60 pour l'une ou l'autre des colonnes (a) et (c), et 48 pour la colonne (b). Ces considérations l'amenèrent à suggérer que l'os d'Ishango serait le plus ancien calendrier lunaire connu.
D'autres caculs
Récemment, l'astrophysicien Jean Paul Mbelek apporta de nouvelles observations :
- La somme de tous les nombres extrêmes des trois colonnes est égale à 60 (10 + 20 + 30 = 60).
- La quantité de nombres de la colonne (b) est égale à la somme des quantités de nombres des colonnes (a) et (c), soit 8 (pour une face) et 4 + 4 = 8(pour l'autre face) ; il existe une régularité plus forte que l'on obtient en ajoutant ou en soustrayant la quantité de nombres apparaissant dans une colonne à la somme totale de cette colonne.
- Il existe une symétrie par rapport à la médiane passant par le nombre 17 et le nombre 10.
Il constate qu'en effet dans la colonne (c) les extrêmes (9 = 10 -1 , 11 = 10 + 1) et les moyens (19 = 20 - 1, 21 = 20 + 1)
« Mathématisme » fantastique ?
Ces trop nombreuses interprétations s'affaiblissent les une les autres : O. Keller, dans un article critiquant les tentations de sur-interpréter les traces archéologiques en histoire des mathématiques[2], qualifie les interprétations de Heinzelin de « fantaisies » et affirme que le groupage de Marshack « paraît très forcé, voire trafiqué ».
Notes et références
- ↑ une telle découverte, bien que rare, n'était pas isolée, et d'autres fossiles pouvant être interpétés comme bâton de comptage sont aujourd'hui connus, tel que par exemple l'os de Lebombo
- ↑ Préhistoire de la géométrie : le problème des sources. Site de l'IREM de La Réunion.
Liens externes
- Le Bâton d'Ishango...23.000 ans...le plus vieil objet mathématique - Institut royal des Sciences naturelles de Belgique
- (en) Eric W. Weisstein. "Ishango Bone." From MathWorld--A Wolfram Web Resource.
- Les os incisés d'Ishango font naître la numération en Afrique, Le Monde, 28 février 2007
- Préhistoire de la géométrie : le problème des sources Article, sur le site de l'Institut de Recherche sur l'Enseignement des Mathématiques, appelant à la prudence quant à l'interprétation des source archéologiques.
- Portail de la République démocratique du Congo
- Portail des mathématiques
- Portail de la Préhistoire
Catégories : Histoire de la République démocratique du Congo | Histoire des mathématiques | Artéfact archéologique
Wikimedia Foundation. 2010.

