Bubble Sort

Exemple du tri à bulles utilisant une liste de nombres aléatoires

Le tri à bulles ou tri par propagation est un algorithme de tri qui consiste à faire remonter progressivement les plus petits éléments d'une liste, comme les bulles d'air remontent à la surface d'un liquide. L'algorithme parcourt la liste, et compare les couples d'éléments successifs. Lorsque deux éléments successifs ne sont pas dans l'ordre croissant, ils sont échangés. Après chaque parcours complet de la liste, l'algorithme recommence l'opération. Lorsqu'aucun échange n'a lieu pendant un parcours, cela signifie que la liste est triée : l'algorithme peut s'arrêter.

Cet algorithme est souvent enseigné en tant qu'exemple algorithmique. Cependant, il présente une complexité en О(n²) dans le pire des cas (où n est la longueur de la liste), ce qui le classe parmi les mauvais algorithmes de tri. Il n'est donc quasiment pas utilisé en pratique.

Complexité

Pour un tableau de taille n, la boucle for sera exécutée n-1 fois et while sera exécutée une fois si permut == faux, c'est-à-dire le tableau est trié n-1 fois si permut est vrai.

• Meilleur cas : O(n) le tableau est trié : n * 1 = o(n)
• Pire cas: o(n²) le tableau est trié en ordre inverse (n -1)*(n-1) = o(n²)

Le nombre d'échanges de paires d'éléments successifs est égal au nombre de couples (i,j) tels que i < j et A(i) > A(j). Ce nombre d'échanges est indépendant de la manière d'organiser les échanges. Pour un tableau aléatoire, il est en moyenne égal à .

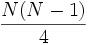Un dérivé du tri à bulles est le shakersort ou tri cocktail. Cette méthode de tri est basée sur une simple observation du comportement du tri à bulles : quand on fait un passage pour trier le maximum du tableau, on a tendance à déplacer les éléments les plus petits du tableau vers le début de celui-ci. Donc l'astuce consiste à alterner les sens de passage de notre bulle. Bien que le nombre d'échanges à effectuer soit identique (voir ci-dessus), on obtient un tri un peu plus rapide que la bulle. En effet, lors des changements de sens, cet algorithme relit les données les plus récentes et qui sont donc encore dans le tampon (cache) de la mémoire. Mais le temps d'exécution est toujours proportionnel à N² donc médiocre.

Notons qu'une variante du tri à bulles, nommée combsort, fut développée en 1980 par Wlodek Dobosiewicz et réapparut en avril 1991 dans Byte Magazine. Elle permet de corriger le défaut majeur du tri à bulles qui sont les tortues et qui rend l'algorithme aussi rapide qu'un quicksort.

Exemple étape par étape

Prenons la liste de chiffres suivante "5 1 4 2 8" et trions-la de manière croissante en utilisant l'algorithme de tri à bulles. Pour chaque étape, les éléments comparés sont écrits en gras.

Première étape:
( 5 1 4 2 8 ) ( 1 5 4 2 8 ) Ici, l'algorithme compare les deux premiers éléments (5 et 1) et les intervertit. (x)
( 1 5 4 2 8 ) ( 1 4 5 2 8 )
( 1 4 5 2 8 ) ( 1 4 2 5 8 )
( 1 4 2 5 8 ) ( 1 4 2 5 8 ) Maintenant que ces deux éléments (5 et 8) sont triés (rangés), l'algorithme ne les intervertira plus.
Deuxième étape:
( 1 4 2 5 8 ) ( 1 4 2 5 8 ) On recommence les mêmes opérations, voir (x)
( 1 4 2 5 8 ) ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
A ce stade, la liste est triée, mais l'algorithme ne sait pas si le travail (le tri) est terminé. L'algorithme doit effectuer un passage sans aucune interversion (échange) pour savoir si le travail est terminé.
Troisième étape:
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
Ici, la liste est triée et l'algorithme peut se terminer.

Implémentations

Une mise en œuvre simple du tri à bulles sur un tableau d'entiers en C :

#define TRUE 1
#define FALSE 0
 
void tri_a_bulle(int t[], int const n) 
{
 	int j   = 0; /* Variable de boucle */
 	int tmp = 0; /* Variable de stockage temporaire */
 
	/* Booléen marquant l'arrêt du tri si le tableau est ordonné */
	int en_desordre = TRUE; 
	/* Boucle de répétition du tri et le test qui
	 arrête le tri dès que le tableau est ordonné(en_desordre=FALSE */
	while(en_desordre)
	{
		/* Supposons le tableau ordonné */
		en_desordre = FALSE;
		/* Vérification des éléments des places j et j+1 */
		for(j = 0 ; j < n- 1 ; j++)
		{
			/* Si les 2 éléments sont mal triés */
			if(t[j] > t[j+1])
			{
				/* Inversion des 2 éléments */
 				tmp = t[j+1];
 				t[j+1] = t[j];
 				t[j] = tmp;
 
 				/* Le tableau n'est toujours pas trié */
				en_desordre = TRUE;
 			}
		}
	}
}

Une amélioration en C++ :

void tri_a_bulle(int *t, int const size) 
{
	bool en_desordre=true;
	for (int i = 0; i < size && en_desordre; ++i)
	{
		en_desordre = false;
		for (int j = 1; j < size - i; ++j)
			if (t[j] > t[j + 1])
			{
				std::swap(t[j+1], t[j]);
				en_desordre = true;
 			}
	}
}

Une implémentation en Pascal (en ordre croissant) :

const
  MAX = 100; (* MAX = 100 est donné en exemple seulement *)
 
type
  tab = array [1..MAX] of integer;
 
procedure TriBulle(n: integer ; var t: tab);
var
  i, j, tmp: integer;
 
begin
  (* On va trier les n-1 premiers éléments du tableau *)
  for i := 1 to n - 1 do
    begin
      for j := 1 to n - i do   (* on fait n-i-1 comparaisons en avançant dans le tableau *)
        begin
          if(t[j + 1] < t[j]) then
             begin
                tmp := t[j];
                t[j] := t[j + 1];
                t[j+1] := tmp;
             end;
        end;
    end;
end;

Une implémentation en Java :

public static void triBulle(int tableau[])
       {
       int longueur=tableau.length;
       boolean permut;
 
       do
           {
           //hypothèse : le tableau est trié
           permut=false;
           for(int i=0;i<longueur-1;i++)
               {
               //Teste si 2 éléments successifs sont dans le bon ordre ou non
               if(tableau[i]>tableau[i+1])
                   {
                   //s'ils ne le sont pas on échange leurs positions
                   echanger(tableau,i,i+1);
                   permut=true;
                   }
               }
            }
       while(permut);
       }

• Une implémentation en PHP :

function bubble_sort($array)
{
    $i = count($array);
    if ($i <= 0) return false;
    $ok = false;
    do
    {
        $ok = true;
        for($j=$i-1; $j>$i; $j–-)
        {
            if ($array[$j] < $array[$j-1])
            {
                $tmp = $array[$j];
                $array[$j] = $array[$j-1];
                $array[$j-1] = $tmp;
                $ok = false;
             }
         }
     }
     while($ok);
     return $array;
}

une implémentation en cobol

       identification division.
           program-id. tribulle.
       environment division.
       data division.
       working-storage section.
           01 tableau-nombres-info.
               05 tabentiers pic 999 occurs 100 times.
           77 maxval pic 99 value 5.
           77 repete pic 999.
           77 i pic 999.
           77 j pic 999.
           77 temp  pic 999.
           77 desordre pic 9 value 1.
 
       procedure division.
      * saisie des valeurs
           perform saisie varying i from 1 by 1
           until i greater than maxval
 
      * affichage des valeurs non triées
           perform affiche varying i from 1 by 1
           until i greater than maxval
           accept temp
 
      * tri du tableau
           PERFORM boucle
           VARYING i FROM 1 BY 1
           UNTIL   (i GREATER THAN maxval) or (desordre equal 0)
           AFTER j from 1 by 1 UNTIL (j GREATER THAN maxval - i).
 
      * affichage des valeurs triées
           perform affiche varying i from 1 by 1
           until i greater than maxval
           accept temp
 
           stop run.
 
       saisie.
           display "Entrez nombre " i ": "
           accept tabentiers (i).
 
       affiche.
           display "nomtre " i ": " tabentiers (i).
 
       boucle.
 
       if tabentiers (j) GREATER THAN tabentiers (j + 1)
           move tabentiers (j) to temp
           move tabentiers (j + 1) to tabentiers (j)
           move temp to tabentiers (j + 1)
           move 1 to desordre.

Optimisation

Exemple de tri à bulles optimisé utilisant une liste d'entiers de 0 à 99 mélangés. Le point rouge représente l'indice du tableau à partir duquel l'algorithme considère que le tableau est trié.

L'algorithme de tri à bulles parcours le tableau jusqu'à ce qu'il n'effectue plus aucune opération sur le tableau. Or, logiquement, à chaque parcours du tableau, on sait que l'élément le plus grand est remonté d'où le nom tri à bulles.

L'algorithme de tri à bulles simple vérifie donc inutilement la partie supérieure du tableau à chaque passage. On peut donc mettre en place une optimisation qui permet donc de ne pas vérifier la partie du tableau déjà triée.

Ce n'est pas le seul avantage de cet optimisation… Imaginons que le tableau soit partiellement trié, lors du premier passage, l'algorithme détectera à partir d'où le tableau est trié, ce qui économisera des opérations…

Exemple pas à pas

Tableau entièrement désordonné

Tableau partiellement trié

Algorithme final

maximum = longeur(tableau)
tant que maximum est supérieur à 0
    maximumTemporaire = 0
    pour i de 0 à maximum - 1
        si la valeur à la position i-1 de tableau
           est supérieure à
           la valeur à la position i   de tableau:
              inverserLesValeursDesPositions(tableau, i, i-1)
              maximumTemporaire = i
    maximum = maximumTemporaire

Liens externes

• Vidéo illustrant le fonctionnement du tri à bulles
• Implémentation en PHP,C,C++,C#,Java

• Portail de l’informatique