Tri par selection

Tri par selection

Tri par sélection

Le tri par sélection (ou tri par extraction) est un des algorithmes de tri les plus triviaux. Il consiste en la recherche soit du plus grand élément (ou le plus petit) que l'on va replacer à sa position finale c'est-à-dire en dernière position (ou en première), puis on recherche le second plus grand élément (ou le second plus petit) que l'on va replacer également à sa position finale c'est-à-dire en avant-dernière position (ou en seconde), etc., jusqu'à ce que le tableau soit entièrement trié.

Le tri par sélection est intéressant lorsque les éléments sont aisément comparables mais coûteux à déplacer dans la structure. Ainsi, le nombre de comparaisons sera toujours supérieur ou égal à ce qui est nécessaire pour effectuer un tri par insertion ou un tri à bulles. Par contre, s'il n'est pas possible de faire des insertions dans la structure en temps constant (O(1)), le nombre d'échanges sera en moyenne très inférieur.

Propriétés

attention ce type de question de CAPES

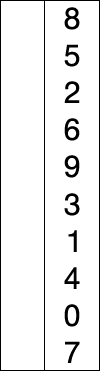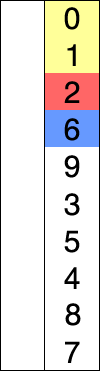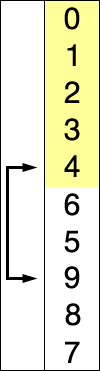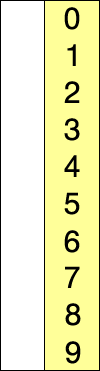Animation représentant le tri par sélection
  • Le nombre de comparaisons nécessaires pour un tri est de N(N-1)/2 (où N est la quantité de donnée à trier).
  • Le nombre d'échanges, lui, est de l'ordre de N.

Le tri par sélection est un tri sur place (les éléments sont triés dans la structure) mais n'est pas un tri stable (l'ordre d'apparition des éléments égaux n'est pas préservé).

Complexité

  • Meilleur cas : O(n2), le tableau est déjà trié, on doit parcourir tout le tableau mais on peut économiser l'échange
  • Pire cas : O(n2), le tableau est trié en ordre inverse
  • Moyenne : O(n2)

Implémentations

Algorithme : (attention « ⇐ » note l'affectation, et « ⇌ » note l'échange de valeur)

 tab_entiers[MAX]

 PROCEDURE selection (tab_entiers t)
    variable c:entier
 	POUR CHAQUE i entier  dans  [0 ;  MAX - 1 [
 		min ⇐ i
 		POUR CHAQUE j entier dans [ i+1 ; MAX [
 			SI t[j] < t[min] ALORS
 				min ⇐ j
 		SI min ≠ i ALORS
                        t[i] ⇌ t[min]

Une mise en œuvre simple du tri par sélection sur un tableau d'entiers en C :

typedef int tab_entiers[MAX];
 
void selection(tab_entiers t)
{
     int i, min, j , x;
     for(i = 0 ; i < MAX - 1 ; i++)
     {
         min = i;
         for(j = i+1 ; j < MAX ; j++)
              if(t[j] < t[min])
                  min = j;
         if(min != i)
         {
             x = t[i];
             t[i] = t[min];
             t[min] = x;
         }
     }
}

Une mise en œuvre simple du tri par sélection sur un tableau d'entiers en Python :

import random
 
MAX_LENGTH = 100
un_tableau = [ k for k in range(0,MAX_LENGTH) ]
random.shuffle(un_tableau)
 
for k in range(0,MAX_LENGTH) :
    min = k
    for l in range(k+1, MAX_LENGTH) :
        if un_tableau[l] < un_tableau[min] :
            min = l
    if min is not k :
        number = un_tableau[k]
        un_tableau[k] = un_tableau[min]
        un_tableau[min] = number

Une mise en œuvre simple du tri par sélection sur un tableau d'entiers en PHP :

 for($i=0;$i<count($arrayOf)-1;$i++)
 {
 	$min = $i;
 	for($j=$i+1;$j<count($arrayOf);$j++)
 	{
 		if($arrayOf[$j] < $arrayOf[$min])
 		{
 				$min = $j;
 		}
 	}	
 
 	if($min != $i)
 	{
 		$x = $arrayOf[$i];
 		$arrayOf[$i] = $arrayOf[$min];
 		$arrayOf[$min] = $x;
 	}							
 }

Le tri par sélection en Pascal (en ordre croissant)

 procedure TriSelection(n : integer ; var t : tab);
 var i, j, min, tmp : integer;
 begin
    for i := 1 to n - 1 do begin
       min := i;
 
       for j := i + 1 to n do
          if (t[j] < t[min]) then min:=j;
 
       if (i <> min) then begin
          tmp := t[i];
          t[i] := t[min];
          t[min] := tmp;
       end;
    end; 
 end;

Le tri par sélection en Java (en ordre croissant) On cherche la plus petite valeur, et on la place au début, etc.

 public void sortBySelection(int[] collection, int sizeOfTheCollection) {
 
 
	int minIndex;
	int tmp;
 
	for (int i=0; i < sizeOfTheCollection; i++) {
 
		minIndex = i;
		tmp = collection[i];
 
		for (int j=i+1; j < sizeOfTheCollection; j++) {
 
			if(collection[j] < collection[minIndex]) {
 
				minIndex = j;
			}
		}
 
		collection[i] = collection[minIndex];
		collection[minIndex] = tmp;
	}
 
 }

Le tri par sélection en Caml (en ordre croissant):

let tri_select t =
  let n = vect_length t and m = ref(0) and i = ref(0) in
     for j=0 to (n - 2) do
       m := t.(j);
       i := j;
       for k = (j + 1) to (n - 1) do
          if !m < t.(k) then begin
                             m:= t.(k);
                             i:= k;
                             end
 
       done;       
   t.(!i) <- t.(j); t.(j) <- !m;
  done;
t;;
Les algorithmes de tri

à bulle • par sélection • par insertion • par tas • par base • rapide • smoothsort • fusion • comptage • de Shell
  • Portail de l’informatique Portail de l’informatique
Ce document provient de « Tri par s%C3%A9lection ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Tri par selection de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Tri par sélection — Le tri par sélection (ou tri par extraction) est un algorithme de tri par comparaison. Il est particulièrement simple, mais inefficace sur de grandes entrées, car il s exécute en temps quadratique en le nombre d éléments à trier. Sommaire 1… …   Wikipédia en Français

  • Tri par dénombrement — Tri comptage Le tri comptage (appelé aussi tri casier) est un algorithme de tri qui s applique sur des valeurs entières. Sommaire 1 Définition 2 Exemple 3 Algorithme 4 Implémentation …   Wikipédia en Français

  • Tri par insertion — Exemple du tri par insertion utilisant une liste de nombres aléatoires Le tri par insertion est un algorithme de tri classique dont le principe est très simple. C est le tri que la plupart des personnes utilisent naturellement pour trier des… …   Wikipédia en Français

  • Tri par base — Le tri par base (ou tri radix) est, en informatique, un algorithme de tri rapide et stable qui peut être utilisé pour ordonner des éléments identifiés par une clef unique. Chaque clef est une chaîne de caractères ou un nombre que le tri par base… …   Wikipédia en Français

  • Tri par tas — Une exécution de l algorithme du tri par tas (Heapsort) trie une partie des valeurs permutées au hasard. Dans un premier temps, les éléments sont réarrangés pour respecter les conditions de tas. Avant le tri à proprement parler, la structure de l …   Wikipédia en Français

  • Tri par paquets — Le tri par paquets est un algorithme de tri qui fonctionne sur des nombres réels appartenant à un intervalle borné fixé à l avance. Le principe de ce tri consiste à diviser l intervalle d entrée en petits sous intervalles identiques et à répartir …   Wikipédia en Français

  • Tri rapide — Le tri rapide (en anglais quicksort) est un algorithme de tri inventé par C.A.R. Hoare en 1961[1] et fondé sur la méthode de conception diviser pour régner. Il est généralement utilisé sur des tableaux, mais peut aussi être adapté aux listes.… …   Wikipédia en Français

  • Tri stable — Algorithme de tri Un algorithme de tri est, en informatique ou en mathématiques, un algorithme qui permet d organiser une collection d objets selon un ordre déterminé. Les objets à trier font donc partie d un ensemble muni d une relation d ordre… …   Wikipédia en Français

  • Selection naturelle — Sélection naturelle Les mécanismes de l évolution biologique Mécanismes non aléatoires: sélection naturelle sélection utilitaire sélection sexuelle sélection de parentèle sélection de groupe s …   Wikipédia en Français

  • Séléction naturelle — Sélection naturelle Les mécanismes de l évolution biologique Mécanismes non aléatoires: sélection naturelle sélection utilitaire sélection sexuelle sélection de parentèle sélection de groupe s …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”