Théorème d'Euler (triangle)

Théorème d'Euler (triangle)

Théorème

Le théorème suivant relatif au triangle quelconque est attribué à Leonhard Euler.

  • La distance entre les centres des cercles inscrit et circonscrit étant notée d,
  • Les rayons des cercles inscrit et circonscrit étant notés respectivement r et R
On a
d^2=R (R-2r) \,


Il résulte en particulier de ce théorème que l'inégalité suivante est également toujours satisfaite :

R \ge 2r.


Démonstration

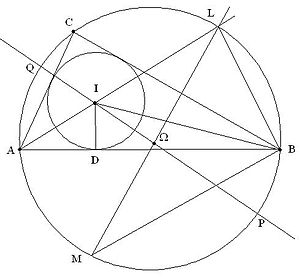
Théorème d'Euler.jpg

Soit ABC le triangle, omega Ω le centre du cercle circonscrit, et I celui du centre du cercle inscrit.

La droite AI coupe le cercle circonscrit en L. Soit M le point diamétralement opposé à L sur ce cercle.

Soit D le pied de la perpendiculaire menée de I sur AB. C'est un point de tangence du cercle inscrit, en sorte qu'on a ID = r.

Les angles LAB et LMB sont égaux, puisqu'ils soutiennent le même arc capable. Les triangles IAD et LBM sont donc semblables puisqu'ils ont deux angles égaux.

On en déduit : \overline{ID} / \overline{LB} = \overline{AI} / \overline{ML},
d'où \overline{ML} \cdot \overline{ID} = \overline{AI} \cdot \overline{LB},
et par conséquent : 2 R r = \overline{AI} \cdot \overline{LB}.

Le triangle BIL est isocèle, et par conséquent BL = BI, et : 2 R r = \overline{AI} \cdot \overline{LI}.

Soient maintenant P et Q les points d'intersection de IΩ avec le cercle circonscrit.

En exprimant de deux manières différentes la puissance du point I par rapport au cercle circonscrit, on obtient :
\overline{PI} \cdot \overline{QI} = \overline{AI} \cdot \overline{LI} = 2 R r.

Par conséquent : (R+d) \cdot (R-d) = 2 R r


Soit encore: R^2 - d^2 = 2 R r \,

et :d^2 = R^2 - 2 R r = R (R-2r)\,

Ce qu'il fallait démontrer.



Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème d'Euler (triangle) de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Théorème d'Euler — Pour les articles homonymes, voir Euler (homonymie). Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le terme théorème d Euler est susceptible de désigner plusieurs théorèmes qui tirent leur nom de… …   Wikipédia en Français

  • Theoreme de Descartes-Euler — Théorème de Descartes Euler Le théorème de Descartes Euler (ou relation d Euler), formulé par Leonhard Euler en 1752, énonce une formule mathématique qui relie le nombre de côtés, de sommets, et de faces dans un polyèdre du genre 0. Un polyèdre… …   Wikipédia en Français

  • Théorème de descartes-euler — Le théorème de Descartes Euler (ou relation d Euler), formulé par Leonhard Euler en 1752, énonce une formule mathématique qui relie le nombre de côtés, de sommets, et de faces dans un polyèdre du genre 0. Un polyèdre de genre 0 est un polyèdre… …   Wikipédia en Français

  • Theoreme de Pythagore — Théorème de Pythagore Une version géométrique du théorème. Le théorème de Pythagore est un théorème de géométrie euclidienne qui énonce que dans un triangle rectangle (qui possède un angle droit) le carré de la longueur de l’hypoténuse (côté… …   Wikipédia en Français

  • Théorème de l'hypoténuse — Théorème de Pythagore Une version géométrique du théorème. Le théorème de Pythagore est un théorème de géométrie euclidienne qui énonce que dans un triangle rectangle (qui possède un angle droit) le carré de la longueur de l’hypoténuse (côté… …   Wikipédia en Français

  • Théorème de pythagore — Une version géométrique du théorème. Le théorème de Pythagore est un théorème de géométrie euclidienne qui énonce que dans un triangle rectangle (qui possède un angle droit) le carré de la longueur de l’hypoténuse (côté opposé à l’angle droit)… …   Wikipédia en Français

  • Triangle — Pour les articles homonymes, voir Triangle (homonymie). Un triangle. En géométrie euclidienne, un trian …   Wikipédia en Français

  • Euler — Leonhard Euler « Euler » redirige ici. Pour les autres significations, voir Euler (homonymie). Leonhard Euler …   Wikipédia en Français

  • Théorème de Descartes-Euler — Le théorème de Descartes Euler (ou relation d Euler), formulé par Leonhard Euler en 1752, énonce une formule mathématique qui relie le nombre de côtés, de sommets, et de faces dans un polyèdre de genre 0 (c est à dire, intuitivement, un polyèdre… …   Wikipédia en Français

  • Triangle isocèle — Triangle Pour les articles homonymes, voir Triangle (homonymie) …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”