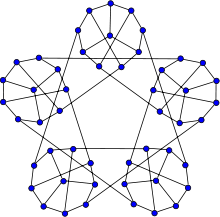
Snark de Szekeres
- Snark de Szekeres
-
Le snark de Szekeres est, en théorie des graphes, un graphe 3-régulier possédant 50 sommets et 75 arêtes.
Propriétés
Propriétés générales
Le diamètre du snark de Szekeres, l'excentricité maximale de ses sommets, est 7, son rayon, l'excentricité minimale de ses sommets, est 6 et sa maille, la longueur de son plus court cycle, est 5. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes.
Coloriage
Le nombre chromatique du snark de Szekeres est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes mais ce nombre est minimal. Il n'existe pas de 2-coloration valide du graphe.
L'indice chromatique du snark de Szekeres est 4. Il existe donc une 4-coloration des arêtes du graphe tels que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Propriétés algébriques
Le groupe d'automorphismes du snark de Szekeres est d'ordre 20.
Le polynôme caractéristique du snark de Szekeres est : (x − 3)(x − 1)9(x + 2)8(x8 − x7 − 12x6 + 10x5 + 41x4 − 25x3 − 43x2 + 13x + 6)4.
Voir aussi
Liens internes
Liens externes
Références
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Snark de Szekeres de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Snark double étoile — Représentation du snark double étoile Nombre de sommets 30 Nombre d arêtes 45 Distribution des degrés 3 régulier Rayon … Wikipédia en Français
Szekeres — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Szekeres: Adrián Szekeres Imre Szekeres Métrique de Kruskal Szekeres Snark de Szekeres Catégorie : Homonymie … Wikipédia en Français
Szekeres snark — infobox graph name = Szekeres snark image caption = namesake = George Szekeres vertices = 50 edges = chromatic number = chromatic index = properties = SnarkIn graph theory, the Szekeres snark is a snark with 50 vertices. It was the fifth known… … Wikipedia
Snark (graph theory) — In graph theory, a snark is a connected, bridgeless cubic graph with chromatic index equal to 4. In other words, it is a graph in which every vertex has three neighbors, and the edges cannot be colored by three colors without two edges of the… … Wikipedia
George Szekeres — Infobox Scientist name = George Szekeres |300px image width = 300px caption = George Szekeres, 2001 birth date = birth date|1911|5|29|mf=y birth place = Budapest, Hungary death date = death date and age|2005|8|28|1911|5|29|mf=y death place =… … Wikipedia
Double-star snark — The Double star snark Vertices 30 Edges 45 Chromatic number … Wikipedia
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Cubic graph — Not to be confused with graphs of cubic functions. The Petersen graph is a Cubic graph … Wikipedia
Diamètre (théorie des graphes) — En théorie des graphes, le diamètre d un graphe est l excentricité maximale de ses sommets, c est à dire la plus grande distance possible qui puisse exister entre deux de ses sommets. L excentricité minimale est appelée rayon. La distance entre… … Wikipédia en Français
Rayon (théorie des graphes) — En théorie des graphes, le rayon d un graphe est l excentricité minimale de ses sommets, c est à dire la plus petite distance à la quelle puisse se trouver un sommet de tous les autres. Le centre d un graphe est formé de l ensemble de ses sommets … Wikipédia en Français