Transformation par polaires réciproques

Transformation par polaires réciproques: Cet article est en travaux depuis 2007... et ne respecte pas les recommandations de présentation encyclopédique. L'article sur la courbe duale apporte le contexte nécessaire à la compréhension de cet article-ci, quasi illisible dans son état actuel.

En mathématiques, et plus précisément en géométrie, la transformation par polaires réciproques est une transformation associant à une courbe une autre courbe construite à l'aide des droites tangentes à la première. La courbe image s'appelle la courbe duale de la courbe de départ.

Sommaire

1 Points cocycliques, quadrilatère inscrit

1.1 Preuve géométrique

1.2 Preuve analytique

2 Un produit scalaire symétrique

2.1 Preuve géométrique

2.2 Preuve analytique

3 Apparition de la droite des tangentes

3.1 preuve analytique

3.2 preuve géométrique

3.3 preuve analytique

4 Polaire réciproque

4.1 Définitions

4.2 Intersection et alignement

5 Polaire d'une courbe

6 Polaire d'une conique

7 Notes et références

8 Voir aussi

8.1 Articles connexes

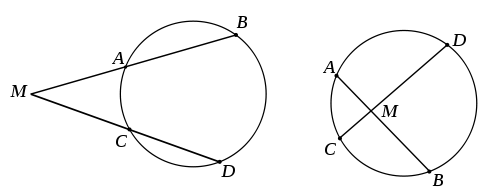
Points cocycliques, quadrilatère inscrit

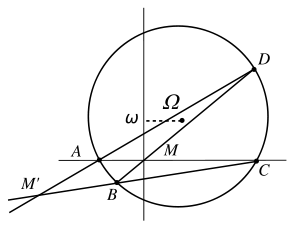
Soit $A, B, C, D$ un quadrilatère et $M$ l'intersection des diagonales.

Les quatre points sont cocycliques si et seulement si $\overline{MA}\,\cdot\,\overline{MB}=\overline{MC}\,\cdot\,\overline{MD}.$

Démonstrations

Preuve géométrique

Dans le sens direct c'est immédiat puisque c'est la puissance de $M$ par rapport au cercle contenant les points.

Réciproquement soit $\mathcal C$ le cercle contenant $A, B, C$ et $D'=(MB)\cap\mathcal C$ Alors $\overline{MD'}=\frac{\overline{MA}\,\overline{MB}}{\overline{MC}}=\overline{MD}$ par hypothèse donc $D = D'$ .

Preuve analytique

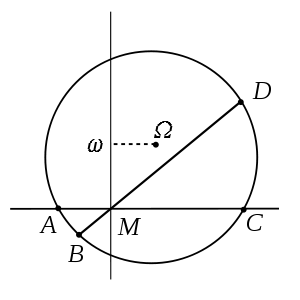
L'origine du plan est prise en $M$ et l'on pose $A (a,0)$ , $C (c,0)$ sur l'axe des abscisses. Un cercle passant par $A$ et $C$ a pour centre $\Omega(\frac{a+c}2,\omega)$ .

On note $b, d$ les abscisses de $B$ et $D$ qui sont donc situés sur une droite $Y = λ X$ .

L'équation du cercle s'écrit $X 2 + Y 2 - (a + c) X - 2ω Y + a c = 0.$

Remplaçant $Y$ par $λ X$ , $B$ et $D$ sont sur le cercle si et seulement si $b$ et $d$ vérifient $(1 + λ 2) X 2 - (a + c + 2λω) X + a c = 0$

L'existence de $\mathcal C$ (i.e. de $ω$ ) équivaut à $bd=\frac{ac}{1+\lambda^2}$ .

Mais $\overline{MB}=\sqrt{1+\lambda^2}b$ et $\overline{MD}=-\sqrt{1+\lambda^2}d$ d'où le résultat.

Un produit scalaire symétrique

PROPRIÉTÉ : Notons $M'$ l'intersection de deux des côtés du quadrilatère. On a

$\overrightarrow{\Omega M}\overrightarrow{\Omega M'}=R^2.$

Démonstrations

Preuve géométrique

$\begin{align}2 MM'^2&=M\Omega^2+\Omega M'^2-2\overrightarrow{\Omega M}\overrightarrow{\Omega M'}\\ \overrightarrow{\Omega M}\overrightarrow{\Omega M'}&=M\Omega^2+\Omega M'^2-MM'^2=M\Omega^2+\Omega M'^2-(\overrightarrow{MA}+\overrightarrow{AM'})(\overrightarrow{MC}+\overrightarrow{CM'}\\ &=R2+\Omega M'^2-\overrightarrow{MA}\cdot\overrightarrow{CM'}-\overrightarrow{AM'}\cdot\overrightarrow{MM'}\\ &=2R^2-\overrightarrow{AM'}\cdot\overrightarrow{DM'}-\overrightarrow{MA}\cdot\overrightarrow{CM'}-\overrightarrow{AM'}\cdot\overrightarrow{MM'}=2R^2- \overrightarrow{MA}\cdot\overrightarrow{CM'}-\overrightarrow{AM'}\cdot\overrightarrow{MD}\end{align}$

en utilisant la puissance de $M$ et $M'$ par rapport au cercle.

Mais, les points $A, B, C, D$ étant cocycliques, $\widehat{BCA}=\widehat{\overrightarrow{MA}\overrightarrow{CM'}}=\widehat{BDA}=\widehat{\overrightarrow{DM}\overrightarrow{AM'}}$

de sorte que $\overrightarrow{MA}\cdot\overrightarrow{CM'}=-\overrightarrow{AM'}\cdot\overrightarrow{MD}\Longleftrightarrow |\!|{ \overrightarrow{MA}}|\!|\,|\!|{\overrightarrow{CM'}}|\!|=|\!|{\overrightarrow{AM'}}|\!|\,|\!|{\overrightarrow{MD}}|\!|$

égalité qui résulte de la relation des sinus dans les triangles $(A M D)$ et $(A C M')$ puisque $\frac{AM}{DM}=\frac{\sin\widehat D}{ \sin\widehat A}=\frac{\sin\widehat C}{\sin(\pi-\widehat A)}=\frac{AM'}{ CM'}.$

Preuve analytique

Supposons $M'=(AD)\cap(BC)$ .

Équation de $(AD)\quad:\quad Y=\lambda\frac{d}{ d-a}(X-a);$

Équation de $(BC)\quad:\quad Y=\lambda\frac{b}{ b-c}(X-c)$

Ce qui donne pour les coordonnées de $M'$

$X=\frac{ad(c-b)-cb(a-d)}{ dc-ab}\quad$ et $\quad Y=\frac{\lambda db(c-a)}{ dc-ab}$ .

Comme $b, d$ sont solutions de l'équation du second degré écrite ci-dessus, (cf. Points cocycliques-Preuve Analytique) on a

$ac=(1+\lambda^2)bd\quad$ et $\quad a+c+2\lambda\omega=(1+\lambda^2)(b+d)$

si bien que $X$ peut aussi s'écrire $X=\frac{bd(c-a)+ac(d-b)}{dc-ab}=\frac{bd[c-a+(1+\lambda^2)(d-b)]}{dc-ab }.$

On a maintenant $\quad \overrightarrow{M\Omega}\overrightarrow{M'\Omega}=\frac{a+c}2\Big(\frac{a+c}2-X\Big)+ \omega(\omega-Y)=\Big(\frac{a+c}2\Big)^2+\omega^2-\frac12(X(a+c)+2\omega Y)$

Or $\quad 2\omega Y=\frac{bd(c-a)}{dc-ab}[(1+\lambda^2)(b+d)-(a+c)]$ ,

d'où l'on tire $\quad X(a+c)+2\omega Y=\frac{(1+\lambda^2)bd[(a+c)(d-b)+(b+d)(c-a)]}{ dc-ab}=2ac$ le crochet faisant $2(d c - a b)$ .

On a donc finalement
$\overrightarrow{M\Omega}\,\overrightarrow{M'\Omega}=\Big(\frac{a+c}2\Big)^2+\omega^2-ac=\Big(\frac{a-c}2\Big)^2+\omega^2=R^2.$

Apparition de la droite des tangentes

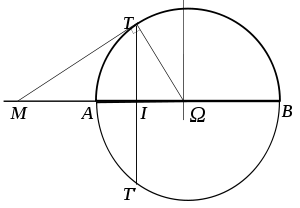
Soit toujours $\mathcal C(\Omega,R)$ un cercle, d'un point $M$ extérieur au cercle on mène les deux tangentes à $\mathcal C$ . Soit $T, T'$ les points de contact.

PROPRIÉTÉ : Si $I=(M\Omega)\cap(TT')$ alors $[M, I]$ divise harmoniquement $[A B]$ .

Démonstrations

preuve analytique

On prend l'origine en $M$ , et $M Ω$ pour axe des abscisses. Le cercle a pour équation $(X - ω) 2 + Y 2 = R 2$ . Les tangentes ont pour équation $Y = λ X$ ce qui donne pour les points de contact $(1 + λ 2) X 2 - 2ω X + ω 2 - R 2 = 0$ équation qui admet donc une racine double (par conséquent $Δ = ω 2 - (ω 2 - R 2)(1 + λ 2) = 0$ ) qui vaut $x_I=\frac\omega{1+\lambda^2}=\frac{\omega^2-R^2}\omega$ qui vérifie bien $\frac2{x_I}=\frac1{\omega-R}+\frac1{\omega+R}$ .

preuve géométrique

$Ω$ étant le milieu de $[A B]$ il suffit de prouver $\overline{\Omega I}\,\overline{\Omega M}=R^2$ (relation de Newton).

Commençons par écrire les trois triangles rectangles $MT^2+R^2=\Omega M^2,\quad MI^2+IT^2=MT^2,\quad IT^2+\Omega I^2=R^2.$

$\overline{\Omega I}\,\overline{\Omega M}=\overline{\Omega I}(\overline{\Omega I}+\overline{IM})=\overline{\Omega I}^2 +\overline{\Omega I}\,\overline{IM}$ . Mais on a $\Omega I^2+IM^2+2\overline{\Omega I}\,\overline{IM}=\Omega M^2=R^2+MI^2+IT^2$ d'où $2\overline{\Omega I}\,\overline{IM}=R^2+IT^2-\Omega I^2$ que l'on reporte pour obtenir
$\Omega I^2+\overline{\Omega I}\,\overline{IM}=\frac12(\Omega I^2+R^2+IT^2)=R^2.$

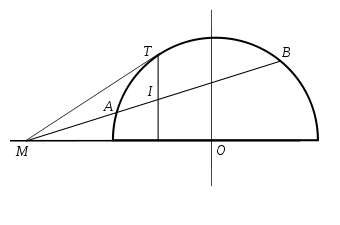
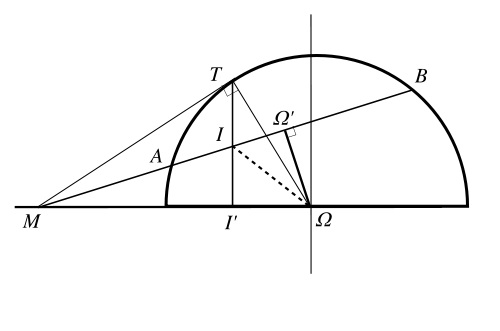
PROPRIÉTÉ : Le point d'intersection de $(T T')$ avec toute corde issue de $M$ divise harmoniquement la corde. $[M I]$ divise harmoniquement $[A B]$

Démonstrations

Soit $I$ le point d'intersection de la corde avec $(T T')$ , $I'$ le projeté de $T$ sur $(Ω M)$ , $Ω'$ le projeté de $Ω$ sur $(A B)$ .

La démonstration proposée repose à nouveau sur plusieurs triangles rectangles.

Comme $Ω'$ est le milieu de $[A B]$ il suffit de prouver que $\overline{\Omega'M}\,\overline{\Omega'I}=\Omega'A^2=R^2-\Omega\Omega'^2$ (relation de Newton) .

De $I'M^2=(\overline{\Omega'M}-\overline{\Omega'I})^2=\Omega'M^2+\Omega'I^2-2\overline{\Omega'M}\,\overline{\Omega'I}^2$ on tire

$\begin{align}2\overline{\Omega'M}\,\overline{\Omega'I}^2&=\Omega'M^2+\Omega'I^2-IM^2=MT^2+R^2-\Omega\Omega'^2+ \omega'I^2-IM^2\\ &=MI'^2+I'T^2-IM^2+\Omega'I^2+R^2-\Omega\Omega'^2=I'T^2+\Omega'I^2-II'^2+R^2-\Omega\Omega'^2\\ &=I'T^2+\Omega I'^2+R^2-2\Omega\Omega'^2=2(R^2-\Omega\Omega'^2)\end{align}$

Il en résulte $\overline{\Omega'M}\,\overline{\Omega'I}^2=R^2-\Omega\Omega'^2=\Omega'A^2$ .

preuve analytique

On prend l'origine en $M$ et l'on note encore $A, B$ la corde et $I$ le point d'intersection. La corde admet toujours une équation de la forme $Y = λ X$ si bien que $\overline{OI}=\sqrt{1+\lambda^2}x_I$ et de même pour $A$ et $B$ .

Pour prouver le résultat, il suffit de le monter pour les abscisses, c'est-à-dire : $\frac2{x_I}=\frac1{a}+\frac1{b}=\frac{a+b}{ab}$ où $a, b$ désignent les abscisses de $A$ et $B$ soit les solutions de l'équation aux intersections $(1 + λ 2) X 2 - 2ω X + ω 2 - R 2 = 0.$

Or on a $a+b=\frac{2\omega}{1+\lambda^2}$ et $ab=\frac{\omega^2-R^2}{1+\lambda^2}$ . Le résultat s'en
suit trivialement.

Polaire réciproque

Cette droite $(T T')$ possède donc les propriétés suivantes :

Toute corde $[A B]$ au cercle, issue d'un point $M$ extérieur à ce cercle, coupe cette droite en un point $I$ tel que $[M I]$ divise harmoniquement $[A B]$ ;

Cette droite et l'ensemble des conjugués harmoniques de $M$ par rapport au cercle;

Pour tout point $I$ de cette droite, le cercle de diamètre $[M I]$ est orthogonal au cercle de départ (cf. cerccles orthogonaux);

Si $O$ est le centre du cercle, $\overrightarrow{OM}\,\overrightarrow{OI}=R^2$ ;

Les intersections des diagonales de tous les quadrilatères complets issues de $M$ sont alignés et sont sur cette droite;

Si dans un repère centré au centre du cercle, le point $M$ a pour coordonnées $(x 0, y 0)$ , l'équation de cette droite est $x 0 X + y 0 Y = R 2$ .

Définitions

Définition : Étant donné un point $M$ et un cercle $\mathcal C$ , on nomme polaire de $M$ par rapport à $\mathcal C$ , l'ensemble des conjugués harmoniques de $M$ par rapport à $\mathcal C$ .

Par conséquent si $M$ est extérieur au cercle, c'est la droite $(T T')$ .

Réciproquement, toute droite du plan est la polaire d'un point unique nommé "pôle" de la droite.

Polaire et pôle sont reliés analytiquement par la relation : $x 0 X + y 0 Y = R 2$ lorsque l'origine du plan est au centre du cercle.

Géométriquement, si la droite $\mathcal D$ coupe le cercle, son pôle ne peut être que le point d'intersection des tangentes au cercle au point $\mathcal D\cap\mathcal C$ . Si la droite ne coupe pas le cercle, on projette le centre $O$ du cercle sur la droite en $I$ ; $M$ est alors le conjugué de $I$ par rapport au cercle, ou bien le projeté sur $(O I)$ d'un point de contact d'une tangente à $\mathcal C$ issue de $I$ , puisqu'il est alors sur la polaire de $I$ .

Intersection et alignement

La "polarisation" échange les notions de droites concourantes et de droite passant par deux points.

PROPRIÉTÉ Soit $M 1, M 2$ deux points (non alignés avec le centre du cercle); si $D 1, D 2$ désignent les polaires de ces points, alors $D_1\cap D_2$ est le pôle de la droite $(M 1 M 2)$ . (Si $M 1, M 2$ sont alignés avec $O$ on obtient le point à l'infini dans la direction perpendiculaire à $(M 1 M 2)$ ).

Démonstrations

Si l'on note $(x i, y i)$ les coordonnées de $M i$ , les coordonnées $(x, y)$ de $D_1\cap D_2$ vérifieront $\left\{\begin{align}x_1x+y_1y&=R^2\\x_2x+y_2y&=R^2\end{align}\right.$ d'où l'on tire

$x=R^2\frac{y_2-y_1}{x_1y_2-x_2y_1}\quad$ et $\quad y=R^2\frac{x_1-x_2}{x_1y_2-x_2y_1}.$

Ce point admet pour polaire la droite d'équation : $\quad R^2X\frac{y_2-y_1}{x_1y_2-x_2y_1}+R^2Y\frac{x_1-x_2}{x_1y_2-x_2y_1}=R^2$

soit la droite $\quad(y_2-y_1)X-(x_2-x_1)Y=x_1y_2-x_2y_1$ ,

qui n'est autre que la droite $(M 1 M 2)$ .

Géométriquement, si $M=D_1\cap D_2$ , les cercles de diamètre $M 1 M$ et $M 2 M$ sont orthogonaux à $\mathcal C$ , donc $M 1$ et $M 2$
sont conjugués de $M$ donc sont situées sur la polaire de $M$ qui est donc la droite $M 1 M 2$ .

PROPRIÉTÉ Soit $D 1, D 2$ deux droites, $M 1, M 2$ leur pôles alors la droite $(M 1 M 2)$ est la polaire du point $D_1\cap D_2$ .

Démonstrations

Les deux droites possèdent des équations que l'on peut mettre sous la forme $a 1 X + b 1 Y = R 2$ et $a 2 X + b 2 Y = R 2$

ce qui fournit les coordonnées des pôles $M 1 (a 1, b 1)$ et $M 2 = (a 2, b 2)$ . La droite $(M 1 M 2)$ a pour équation $(b 2 - b 1) X - (a 2 - a 1) Y = a 1 b 2 - a 2 b 1$

son pôle a donc pour coordonnées
$X=R^2\frac{b_1-b_2}{a_1b_2-a_2b_1}\qquad$ et $\qquad Y=R^2\frac{a_2-b_1}{a_1b_2-a_2b_1}$ qui est précisément le point commun aux deux droites.

Polaire d'une courbe

Il y a deux façons naturelles de définir la polaire d'une courbe.

Ou bien à un point $M$ de la courbe on associe sa polaire puis l'on considère l'enveloppe de ces polaires ou bien on considère le lieu formé par les pôles des tangentes à la courbe. Ces deux notions coincident.

Soit $(x (t), y (t))$ une courbe du plan, la tangente a pour équation $X y' - Y x' = x y' - y x'$ son pôle a donc pour coordonnées

$X_0(t)=\frac{R^2y'}{xy'-yx'}$ et $Y_0(t)=\frac{-R^2x'}{xy'-yx'}.$

La polaire du point $(x (t), y (t))$ a pour équation $X x (t) + Y y (t) = R 2$ . L'enveloppe de cette famiille de droites est déterminée par les équations $\left\{\begin{align}X_0x(t)+Y_0y(t)&=R^2\\X_0x'(t)+Y_0y'(t)&=0\end{align}\right.$ qui donne précis&ément les mêmes expressions que précédemment.

La "polarisation" échange donc les notions de point d'une courbe et de tangente à la courbe.

Polaire d'une conique

PROPRIÉTÉ : La polaire d'une conique par rapport à un cercle centré en un foyer de la conique est un cercle centré au pôle de la directrice.

Démonstrations

L'origine étant prise au foyer, on définit la conique par son équation polaire $\rho=\frac p{1-e\cos\theta}$ Le pôle d'une tangente est situé sur la perpendiculaire à celle-ci passant par le foyer (l'origine). Il a donc pour angle polaire $\theta+V+\frac\pi2$ où $V$ désigne l'angle entre $(O M)$ et la tangente.

On sait maintenant que le pôle est en division harmonique avec le projeté du foyer sur la tangente et l'intersection avec le cercle.

La distance du foyer à la tangente vaut $d=\rho\cos(V+\frac\pi2)=-\rho\sin V$ le pôle cherché est donc à la distance $\frac{R^2}d$

Les coordonnées du pôle sont donc $x=\frac{R^2}d\cos(\theta+V+\frac\pi2)=\frac{R^2}\rho\Big[\frac{\sin\theta}{\tan V}+\cos\theta\Big]$

et $y=\frac{R^2}d\sin(\theta+V+\frac\pi2) =\frac{R^2}\rho\Big[\frac{\sin\theta}{\tan V}+\cos\theta\Big]$

Mais $\ \tan V=\frac\rho{\rho'}=-\frac{1-e\cos\theta}{e\sin\theta}$

d'où $x=\frac{R^2}p(1-e\cos\theta)\Big[\frac{e\sin^2\theta}{1-e\cos\theta}+\cos\theta\Big]=\frac{R^2}p(\cos\theta-e)$

et $y=-\frac{R^2}p(1-e\cos\theta)\Big[-\frac{e\sin\theta\cos\theta}{1-e\cos\theta}-\sin\theta\Big] =-\frac{R^2}p\sin\theta$

d'où il résulte sans peine : $\Big(x+\frac{eR^2}p\Big)^2+y^2=\frac{R^4}{p^2}.$

On obtient donc bien un cercle de centre $\Big(\frac{eR^2}p,O\Big)$ qui est le pôle de la droite
d'équation $X=-\frac pe$ c'est-à-dire la directrice.

Notes et références

Voir aussi

Articles connexes

théorème de Pascal

Courbe duale

Portail de la géométrie

Catégories :
Géométrie
Géométrie projective
Transformation géométrique

Contenu soumis à la licence CC-BY-SA. Source : Article Transformation par polaires réciproques de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Transformation conforme — En mathématiques, et plus précisément en géométrie et en analyse complexe, une transformation conforme est une transformation qui conserve les angles. Une France conforme, et... anticonforme Sommaire 1 Cas du plan … Wikipédia en Français
Courbe duale — Courbes duales l une de l autre. En mathématiques, et plus précisément en géométrie projective, la courbe duale d une courbe plane donnée est une courbe associée à la première par dualité. On peut la considérer de manière informelle comme l… … Wikipédia en Français
polaire — [ pɔlɛr ] adj. et n. f. • 1555; bas lat. polaris → pôle 1 ♦ Relatif aux pôles célestes, terrestres; situé près d un pôle. L étoile Polaire, ou n. f. la Polaire, qui indique la direction du nord. Régions, zones polaires, situées près du pôle… … Encyclopédie Universelle
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
LIE (S.) — À la fin du XIXe siècle, le mathématicien norvégien Marius Sophus Lie a posé les fondements d’une des théories les plus centrales des mathématiques contemporaines, la théorie des groupes de Lie, dont la puissance s’est révélée considérable, et… … Encyclopédie Universelle
polarité — [ pɔlarite ] n. f. • 1765 « propriété qu a l aimant de se diriger vers les pôles »; de polaire ♦ Sc. 1 ♦ Math., phys. État d un système dont deux points quelconques présentent des caractéristiques différentes (opposées ou distinctes). 2 ♦ Biol.… … Encyclopédie Universelle
dual — dual, duale [ dɥal; dyal ] adj. • 1948; du bas lat. dualis « deux » 1 ♦ Log., math. Se dit de propriétés qui sont par deux et qui présentent un caractère de réciprocité. Équation, expression duale, qui se déduit d une équation ou d une expression … Encyclopédie Universelle
Dualité (Géométrie Projective) — La dualité projective, crée par Jean Victor Poncelet (1788 1867), père fondateur de la géométrie projective, bien que beaucoup moins enseignée que la dualité en algèbre linéaire, est probablement la plus belle notion de dualité que l on rencontre … Wikipédia en Français
Dualité (géométrie projective) — Pour les articles homonymes, voir Dualité (mathématiques) et Dualité. La dualité projective, crée par Jean Victor Poncelet (1788 1867), père fondateur de la géométrie projective, bien que beaucoup moins enseignée que la dualité en algèbre… … Wikipédia en Français
Geometrie projective — Géométrie projective La géométrie projective est le domaine des mathématiques qui modélise les notions intuitives de perspective et d horizon. Elle étudie les propriétés des figures inchangées par projection. Sommaire 1 Considérations historiques … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Transformation par polaires réciproques

Sommaire

Points cocycliques, quadrilatère inscrit

Preuve géométrique

Preuve analytique

Un produit scalaire symétrique

Preuve géométrique

Preuve analytique

Apparition de la droite des tangentes

preuve analytique

preuve géométrique

preuve analytique

Polaire réciproque

Définitions

Intersection et alignement

Polaire d'une courbe

Polaire d'une conique

Notes et références

Voir aussi

Articles connexes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Transformation par polaires réciproques

Sommaire

Points cocycliques, quadrilatère inscrit

Preuve géométrique

Preuve analytique

Un produit scalaire symétrique

Preuve géométrique

Preuve analytique

Apparition de la droite des tangentes

preuve analytique

preuve géométrique

preuve analytique

Polaire réciproque

Définitions

Intersection et alignement

Polaire d'une courbe

Polaire d'une conique

Notes et références

Voir aussi

Articles connexes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link