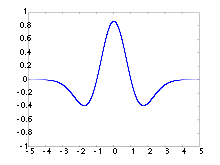
- Ondelette chapeau mexicain
-
En mathématiques et en analyse numérique, l'ondelette chapeau mexicain.
est le négatif normalisé de la dérivée seconde d'une fonction gaussienne, c'est-à-dire, à l'échelle et à la normalisation près, la seconde d'un polynôme d'Hermite. Elle est un cas particulier de la famille des ondelettes continues(l'ondelette utilisée dans la transformée en ondelettes continue) connue sous le nom ondelettes hermitienne. Elle est généralement dénommée "chapeau mexicain" aux États-Unis, car la forme de sa courbe rappelle un chapeau typique du Mexique, le "sombrero". Dans la nomenclature technique, cette fonction est connue sous le nom d'ondelettes Ricker, où elle est souvent utilisée pour le traitement des données sismiques.
La généralisation à plusieurs dimensions de cette ondelette est appelée fonction laplacienne de Gauss. Dans la pratique, cette ondelette est parfois approchée par une différence de gaussiennes, car elle est séparable et peut donc gagner un temps de calcul très important. L'échelle normalisée Laplacien (en L 1-norme) (en L1-norm) est fréquemment utilisé comme un détecteur de blob et pour la sélection automatique de l'échelle dans la vision par ordinateur des applications, voir laplacien de gaussien et de la théorie de l'espace d'échelle. L'ondelette chapeau mexicain peut également être approché par des dérivés du Cardinal B-Splines[1]
References
- Brinks R: On the convergence of derivatives of B-splines to derivatives of the Gaussian function, Comp. Appl. Math., 27, 1, 2008
Wikimedia Foundation. 2010.