Graphe de de Bruijn

Graphe de de Bruijn

Un graphe de de Bruijn est un graphe orienté défini par le mathématicien Nicolaas Govert de Bruijn en 1946. Un graphe de de Bruijn permet de représenter les chevauchements de longueur L-1 entre tous les mots de longueur L d'un langage.

Soit un alphabet \mathfrak{A}=\{\alpha_1, \dots, \alpha_n\} de taille n. On note Gn,L = (S,A) le graphe de de Bruijn d'ordre L construit sur l'alphabet \mathfrak{A}. Les sommets S de Gn,L représentent (sont étiquetés) les Ln mots de longueur L construits à partir des lettres de l'alphabet \mathfrak{A} :

S=\{\alpha_1^L,\ \alpha_1^{L-1}\alpha_2,\ \dots,\ \alpha_1^{L-1}\alpha_n, \dots,\ \alpha_n^L\}.

Il existe un arc Ai,j allant du sommet si (représentant le mot u=u_1\dots u_L) au sommet sj (représentant le mot v=v_1\dots v_L) du graphe Gn,L si

u_2\dots u_L=v_1\dots v_{L-1}, soit uk = vk − 1 pour k=2,…, L.

Autrement dit, il existe un arc (si,sj) dans A si le suffixe de longueur L-1 du mot u et le préfixe de longueur L-1 du mot v correspondent.

Exemple

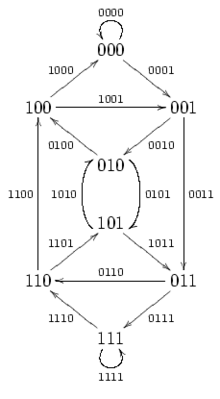
Graphe de de Bruijn G2,3 construit sur un alphabet binaire (n=2) pour des mots de longueur L=3.

Le graphe G2,3 = (S,A) ci-contre est construit sur un alphabet binaire \mathfrak{A}=\{0, 1\} pour des mots de longueur L=3. Il existe 23 = 8 mots de longueur 3 sur un alphabet binaire :

S=\{000,\ 001,\ 010,\ 011,\ 111,\ 110,\ 101,\ 100\}.

Il existe un arc allant du sommet 000 au sommet 001 car le suffixe de longueur 2 (L-1) de 000 est égal au préfixe de longueur 2 de 001. Il existe un arc allant du sommet 100 au sommet 000 car le suffixe de longueur 2 de 100 est égal au préfixe de longueur 2 de 000.

Propriétés

Chaque sommet d'un graphe de de Bruijn construit sur un alphabet n-aire a n arcs sortants (choix de la dernière lettre). De même, chaque sommet a n arcs rentrants.

Un graphe de de Bruijn est eulérien.

Utilisation

Les graphes de de Bruijn sont utilisés en bioinformatique pour l'assemblage de novo de reads (ou lectures) issues d'un séquençage.


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Graphe de de Bruijn de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Graphe (mathématiques) — Théorie des graphes  Pour la notion mathématique utilisée en Théorie des ensembles, voir Graphe d une fonction. La théorie des graphes est une branche commune à l informatique et aux mathématiques étudiant les graphes et les objets qui lui… …   Wikipédia en Français

  • Graphe (théorie des graphes) — Théorie des graphes  Pour la notion mathématique utilisée en Théorie des ensembles, voir Graphe d une fonction. La théorie des graphes est une branche commune à l informatique et aux mathématiques étudiant les graphes et les objets qui lui… …   Wikipédia en Français

  • Nicolaas Govert de Bruijn — Pour les articles homonymes, voir De Bruijn. De Bruijn à Oberwolfach, dans les années 1960 Nicolaas Govert de Bruijn (né le 9 juillet 1918) est un mathématicien …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Theorie des graphes — Théorie des graphes  Pour la notion mathématique utilisée en Théorie des ensembles, voir Graphe d une fonction. La théorie des graphes est une branche commune à l informatique et aux mathématiques étudiant les graphes et les objets qui lui… …   Wikipédia en Français

  • Théorie des graphes — Pour la notion mathématique utilisée en Théorie des ensembles, voir Graphe d une fonction. La théorie des graphes est une théorie informatique et mathématique. Les algorithmes élaborés pour résoudre des problèmes concernant les objets de cette… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Claw-free graph — A claw In graph theory, an area of mathematics, a claw free graph is a graph that does not have a claw as an induced subgraph. A claw is another name for the complete bipartite graph K1,3 (that is, a star graph with three edges, three leaves, and …   Wikipedia

  • Edge coloring — A 3 edge coloring of the Desargues graph. In graph theory, an edge coloring of a graph is an assignment of “colors” to the edges of the graph so that no two adjacent edges have the same color. For example, the figure to the right shows an edge… …   Wikipedia

  • Assistant de preuve — En informatique (ou en mathématiques assistées par informatique), un assistant de preuve est un logiciel permettant l écriture et la vérification de preuves mathématiques, soit sur des théorèmes au sens usuel des mathématiques, soit sur des… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”