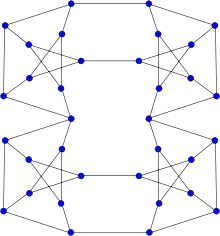
34-graphe de Thomassen
- 34-graphe de Thomassen
-
Le 34-graphe de Thomassen est, en théorie des graphes, un graphe possédant 34 sommets et 52 arêtes.
Propriétés
Propriétés générales
Le diamètre du 34-graphe de Thomassen, l'excentricité maximale de ses sommets, est 7, son rayon, l'excentricité minimale de ses sommets, est 7 et sa maille, la longueur de son plus court cycle, est 5. Il s'agit d'un graphe 2-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 2 sommets ou de 3 arêtes.
Coloriage
Le nombre chromatique du 34-graphe de Thomassen est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal.
L'indice chromatique du 34-graphe de Thomassen est 4. Il existe donc une 4-coloration des arêtes du graphe tels que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Propriétés algébriques
Le polynôme caractéristique du 34-graphe de Thomassen est : (x − 1)8(x + 2)5(x2 − 3)2(x2 − 2x − 1)(x2 + 2x − 1)2(x3 − 2x2 − 3x + 2)(x4 − 9x2 − 2x + 12)(x4 − 2x3 − 7x2 + 10x + 4).
Voir aussi
Liens internes
Liens externes
Références
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article 34-graphe de Thomassen de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
105-graphe de Thomassen — Nombre de sommets 105 Nombre d arêtes 170 Distribution des degrés 3 (85 sommets) 4 (15 sommets) 5 (5 sommets) Rayon 8 Diamètre 9 Maille 5 Nombre chromatique 3 … Wikipédia en Français
32-graphe de Thomassen — Nombre de sommets 32 Nombre d arêtes 53 Distribution des degrés 3 (24 sommets) 4 (6 sommets) 5 (2 sommets) Rayon 4 Diamètre 6 Maille 4 Nombre chromatique 3 … Wikipédia en Français
60-graphe de Thomassen — Représentation du 60 graphe de Thomassen. Nombre de sommets 60 Nombre d arêtes 99 Distribution des degrés 3 (42 sommets) 4 (18 sommets) … Wikipédia en Français
20-graphe de Thomassen — Nombre de sommets 20 Nombre d arêtes 33 Distribution des degrés 3 (15 sommets) 4 (4 sommets) 5 (1 sommet) Rayon 3 Diamètre 4 Maille 5 Nombre chromatique 3 … Wikipédia en Français
41-graphe de Thomassen — Nombre de sommets 41 Nombre d arêtes 64 Distribution des degrés 3 (38 sommets) 4 (2 sommets) 6 (1 sommet) Rayon 5 Diamètre 8 Maille 5 Nombre chromatique 3 … Wikipédia en Français
94-graphe de Thomassen — Nombre de sommets 94 Nombre d arêtes 141 Distribution des degrés 3 régulier Rayon 9 Diamètre 12 Maille 4 Nombre chromatique 3 … Wikipédia en Français
Graphe de Hatzel — Nombre de sommets 57 Nombre d arêtes 88 Distribution des degrés 3 (52 sommets) 4 (5 sommets) Rayon 7 Diamètre 8 Maille 4 Automorphismes 8 Nombr … Wikipédia en Français
Graphe de Wiener-Araya — Représentation du graphe de Wiener Araya. Nombre de sommets 42 Nombre d arêtes 67 Distribution des degrés 3 (34 sommets) 4 (8 sommets) Maille … Wikipédia en Français
Graphe hypohamiltonien — En théorie des graphes, un graphe est hypohamiltonien s il n a pas de cycle hamiltonien mais que la suppression de n importe quel sommet du graphe suffit à le rendre hamiltonien. Sommaire 1 Histoire 2 Planarité 3 Exemples … Wikipédia en Français
48-graphe de Zamfirescu — Représentation du 48 graphe de Zamfirescu. Nombre de sommets 48 Nombre d arêtes 76 Distribution des degrés 3 (40 sommets) 4 (8 sommets) Rayon 6 … Wikipédia en Français