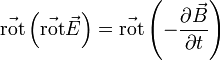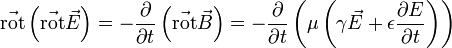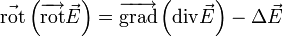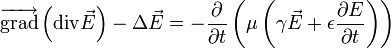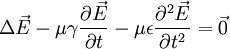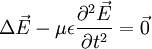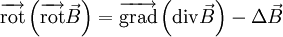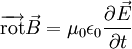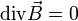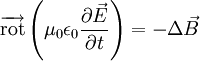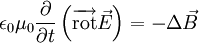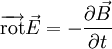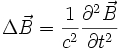Établissement de l'équation de propagation à partir des équations de maxwell

Établissement de l'équation de propagation à partir des équations de Maxwell

L'équation de propagation d'une onde électromagnétique peut se calculer à partir des équations de Maxwell.

Équation relative au champ électrique $E$

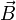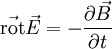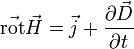Pour éliminer le champ magnétique $\vec B$ entre $\vec{\operatorname{rot}} \vec E = - \frac{\partial \vec B}{\partial t}$ et $\vec{\operatorname{rot}} \vec H = \vec j + \frac{\partial \vec D}{\partial t}$ , il suffit de remplacer 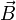$\vec B$ dans la première équation par son expression en fonction de 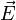$\vec E$ . Pour cela, comme 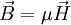$\vec B = \mu \vec H$ peut être obtenu par son rotationnel (deuxième équation), il est donc judicieux de faire apparaître 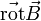$\vec{\operatorname{rot}} \vec B$ au second membre de la première équation, en considérant le rotationnel des deux membres de cette équation.

$\vec{\operatorname{rot}} \left( \vec{\operatorname{rot}} \vec{E} \right) = \vec{\operatorname{rot}} \left( - \frac{\partial \vec B}{\partial t} \right)$

Grâce au théorème de Schwarz on peut permuter les opérateurs spatiaux et temporels ainsi qu'en remplaçant avec l'expression du rotationnel de 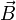$\vec B$ selon maxwell :

$\vec{\operatorname{rot}} \left( \vec{\operatorname{rot}} \vec{E} \right) = - \frac{\partial}{\partial t} \left( \vec{\operatorname{rot}} \vec B \right) = - \frac{\partial}{\partial t} \left( \mu \left( \gamma \vec E + \epsilon \frac{\partial E}{\partial t} \right) \right)$

En utilisant les propriétés des opérateurs vectoriels, soit :

$\vec{\operatorname{rot}}\left(\overrightarrow\operatorname{rot}\vec{E}\right) = \overrightarrow\operatorname{grad}\left(\operatorname{div}\vec{E}\right)-\Delta\vec{E}$

nous obtenons alors :

$\overrightarrow\operatorname{grad}\left(\operatorname{div}\vec{E}\right)-\Delta\vec{E} = - \frac{\partial}{\partial t} \left( \mu \left( \gamma \vec E + \epsilon \frac{\partial E}{\partial t} \right) \right)$

Pour un milieu non chargé, ou chargé de manière uniforme, 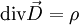$\operatorname{div} \vec D = \rho$ , une constante, dont le divergeant sera nul. Dans ce cas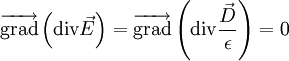 $\overrightarrow\operatorname{grad}\left(\operatorname{div}\vec{E}\right) = \overrightarrow\operatorname{grad}\left(\operatorname{div}\frac{\vec{D}}{\epsilon}\right) = 0$

D'où finalement, l'équation d'onde relative au champ électrique $\vec E$

$\Delta\vec{E} - \mu \gamma \frac{\partial \vec E}{\partial t} - \mu \epsilon \frac{\partial^2 \vec E}{\partial t ^2} = \vec 0$

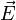
Cette relation se simplifie dans un milieu parfait isolant illimité et non chargé. Dans ce cas, $γ = 0$ , ce qui donne :

$\Delta\vec{E} - \mu \epsilon \frac{\partial^2 \vec E}{\partial t ^2} = \vec 0$

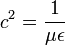
Ou encore, en posant $c^2=\frac{1}{\mu \epsilon}$

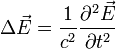
$\Delta\vec{E} = \frac{1}{c^2} \frac{\partial^2 \vec E}{\partial t ^2}$

Pour le champ $B$

La démonstration suivante suppose que le milieu considéré est le vide. On part de la relation :

$\overrightarrow\operatorname{rot}\left(\overrightarrow\operatorname{rot}\vec{B}\right) = \overrightarrow\operatorname{grad}\left(\operatorname{div} \vec{B}\right)-\Delta\vec{B}$

dans le vide, la densité de courant étant nulle, l'équation de Maxwell-Ampère s'écrit :

$\overrightarrow\operatorname{rot}\vec{B}=\mu_0\epsilon_0\frac{\partial\vec{E}}{\partial t}$

soit :

$\operatorname{div} \vec{B}=0$

La relation initiale devient alors :

$\overrightarrow\operatorname{rot}\left(\mu_0\epsilon_0\frac{\partial\vec{E}}{\partial t}\right) = -\Delta\vec{B}$

Grâce au théorème de Schwarz on peut permuter les opérateurs spatiaux et temporels et on a :

$\epsilon_0\mu_0\frac{\partial}{\partial t}\left(\overrightarrow\operatorname{rot}\vec{E}\right) = - \Delta\vec{B}$

On peut alors utiliser l'équation de Maxwell-Faraday :

$\overrightarrow\operatorname{rot}\vec{E}=-\frac{\partial\vec{B}}{\partial t}$

On obtient alors à partir de la relation initiale, avec la relation $ε 0 μ 0 c 2 = 1$ :

$\Delta\vec{B} = \frac{1}{c^{2}} \frac{\partial^{2}\vec{B}}{\partial t^{2}}$

Voir aussi

Portail de la physique
Portail de l’électricité et de l’électronique

Ce document provient de « %C3%89tablissement de l%27%C3%A9quation de propagation %C3%A0 partir des %C3%A9quations de Maxwell ».

Catégories : Outils théoriques de l'électromagnétisme | Mécanique ondulatoire

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Établissement de l'équation de propagation à partir des équations de maxwell de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Etablissement de l'equation de propagation a partir des equations de Maxwell — Établissement de l équation de propagation à partir des équations de Maxwell L équation de propagation d une onde électromagnétique peut se calculer à partir des équations de Maxwell. Équation relative au champ électrique E Pour éliminer le champ … Wikipédia en Français
Établissement de l'équation de propagation à partir des équations de Maxwell — L équation de propagation d une onde électromagnétique peut se calculer à partir des équations de Maxwell. Sommaire 1 Hypothèses préalables 2 Formulation des relations 2.1 Équation relative au champ électrique E … Wikipédia en Français
Equations de Maxwell — Équations de Maxwell Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… … Wikipédia en Français
Équations de Maxwell pour les nuls — Équations de Maxwell Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… … Wikipédia en Français
Équations de maxwell — Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l électromagnétisme, avec l… … Wikipédia en Français
Équations de Maxwell — Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l électromagnétisme, avec l… … Wikipédia en Français
Maxwell-Faraday — Équations de Maxwell Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… … Wikipédia en Français
Équation de Maxwell — Équations de Maxwell Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… … Wikipédia en Français
Équation de Maxwell-Gauss — Équations de Maxwell Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… … Wikipédia en Français
Équations des ondes électromagnétiques — Équations de Maxwell Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Établissement de l'équation de propagation à partir des équations de maxwell