Équation différentielle Générale autonome du premier ordre

Équation différentielle Générale autonome du premier ordre

Équation différentielle autonome

Une équation différentielle autonome est un cas particulier important d'équation différentielle où la variable n'apparaît pas dans l'équation fonctionnelle. C'est une équation de la forme :

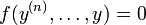
f(y^{(n)},\dots,y)=0

Les lois de la physique s'appliquent en général à des fonctions du temps, et se présentent sous forme d'équations différentielles autonomes, ce qui manifeste l'invariance de ces lois dans le temps. Ainsi, si un système autonome revient à sa position initiale au bout d'un intervalle de temps T, il connaît dès lors une évolution périodique de période T.

L'étude des équations autonomes est équivalente à celle des champs de vecteurs. Pour une équation du premier ordre, les solutions sont une famille de courbes qui ne se coupent pas (d'après le théorème de Cauchy-Lipschitz) et qui remplissent l'espace. Elles sont tangentes au champ de vecteurs en chaque point.

Résolution par les Séries de Taylor

Pour résoudre par les séries de Taylor, il nous faut tout d’abord ajouter une condition initiale. Et sans perte de généralité, posons cette condition comme étant:

y(0) = 0

En utilisant la théorie des espèces de structures appliquée aux équations différentielles nous calculons la solution de la façon suivante:

Soit (*)

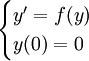
\begin{cases}y' = f(y) \\ y(0) = 0 \end{cases}

une équation différentielle générale autonome d'ordre 1 accompagnée d'une condition initiale. Exprimons tout d'abord la fonction f en série de Taylor. Ainsi

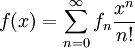
f(x) = \sum^{\infty}_{n=0} f_n\frac{x^n}{n!}

Alors la solution de (*) est donnée par la série de Taylor suivante :

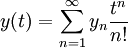
y(t) = \sum^{\infty}_{n=1} y_n\frac{t^n}{n!}

avec

y1 = f0

et

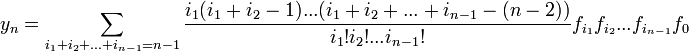
y_n = \sum^{}_{i_1+i_2+...+i_{n-1}=n-1} \frac{i_1(i_1+i_2-1)...(i_1+i_2+...+i_{n-1} - (n-2))}{i_1!i_2!...i_{n-1}!}f_{i_1}f_{i_2}...f_{i_{n-1}}f_0

Système différentiel autonome

Un système de deux équations différentielles autonomes du premier ordre est un système de la forme

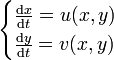
\begin{cases} \frac{\mathrm dx}{\mathrm dt} = u(x,y) \\ \frac{\mathrm dy}{\mathrm dt} = v(x,y) \end{cases}

avec u et v continues sur un ouvert Ω de 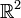\R^2. On observe immédiatement qu'il est indépendant de t. Ce système peut être transformé en une équation différentielle en y :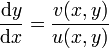

\frac{\mathrm dy}{\mathrm dx} = \frac{v(x,y)}{u(x,y)}
  • Portail des mathématiques Portail des mathématiques

Bibliographie

  • Jean-François Gagné (dir. Gilbert Labelle), Rapport existant entre la théorie des espèces et les équations différentielles, Université du Québec à Montréal (Mémoire de maîtrise en mathématiques), 1985, 110 pages, [M1216].
Ce document provient de « %C3%89quation diff%C3%A9rentielle autonome ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Équation différentielle Générale autonome du premier ordre de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Equation differentielle Generale autonome du premier ordre — Équation différentielle autonome Une équation différentielle autonome est un cas particulier important d équation différentielle où la variable n apparaît pas dans l équation fonctionnelle. C est une équation de la forme : Les lois de la… …   Wikipédia en Français

  • Équation différentielle générale autonome du premier ordre — Équation différentielle autonome Une équation différentielle autonome est un cas particulier important d équation différentielle où la variable n apparaît pas dans l équation fonctionnelle. C est une équation de la forme : Les lois de la… …   Wikipédia en Français

  • Équation différentielle autonome — Une équation différentielle autonome est un cas particulier important d équation différentielle où la variable n apparaît pas dans l équation fonctionnelle. C est une équation de la forme : Les lois de la physique s appliquent en général à… …   Wikipédia en Français

  • Équation différentielle du premier ordre — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… …   Wikipédia en Français

  • Equation differentielle — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… …   Wikipédia en Français

  • Equation différentielle — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… …   Wikipédia en Français

  • Équation différentielle ordinaire — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… …   Wikipédia en Français

  • Équation différentielle — En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de dérivation auquel l une des fonctions inconnues a… …   Wikipédia en Français

  • Theoreme de Cauchy-Lipschitz — Théorème de Cauchy Lipschitz Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le …   Wikipédia en Français

  • Théorème de Cauchy-Lipschitz — Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. En mathématiques, et plus précisément en a …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”