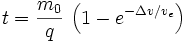Équation de Tsiolkowski

L'équation de Tsiolkowski est l'équation fondamentale de l'astronautique reliant l'accroissement de vitesse au cours d'une phase de propulsion d'un astronef doté d'un moteur à réaction au rapport de ses masses initiales et finales.

On la doit à Constantin Tsiolkovski et, indépendamment, à Hermann Oberth.

Énoncé

Plus précisément la loi s'énonce ainsi :

dans laquelle :

• Δv est la variation de vitesse entre le début et la fin de la phase propulsée considérée, exprimée en m/s ;
• v_e est la vitesse d'éjection des gaz, exprimée en m/s ;
• m₀ est la masse totale de l'astronef au début de la phase propulsée ;
• m₁ est la masse totale de l'astronef à l'issue de la phase propulsée, exprimée dans la même unité que m₀.

Cette équation est établie en intégrant l'équation de conservation de la quantité de mouvement entre le début et la fin de la phase propulsée sous les hypothèses suivantes :

• l'étude du mouvement est faite dans un référentiel d'inertie ;
• l'astronef n'est soumis qu'à la force de poussée fournie par ses moteurs, aucune autre action extérieure (gravité, efforts aérodynamiques) n'est prise en compte ;
• le débit massique d'ergol est constant pendant la phase de propulsion ;
• la vitesse d'éjection des gaz est elle aussi constante.

L'équation est valable aussi bien lors d'une phase d'accélération (la poussée est de sens opposé à la vitesse, Δv est alors l'accroissement de vitesse) ou de décélération (la poussée est de même sens que la vitesse, Δv est la réduction de vitesse).

Elle est aussi valable dans le cas où la phase propulsée est réalisée aux moyens de plusieurs étages allumés successivement l'un après l'autre. C'est d'ailleurs cette propriété qui explique le choix de concevoir des fusées à plusieurs étages propulsifs. L'accroissement de vitesse n'étant fonction que du rapport de la masse initiale sur la masse finale (indépendamment de la vitesse d'éjection des gaz qui est elle fixée par la technologie des moteurs employés), on a tout intérêt à ce que la masse structurelle finale de l'astronef soit la plus petite possible, le seul moyen d'y arriver étant de se débarrasser en cours de propulsion de la masse structurelle des étages devenus inutiles une fois vidés de la totalité de leurs ergols.

Malgré l'apparente simplicité de cette équation et des hypothèses qui la sous-tendent, elle constitue une approximation utile au calcul des manœuvres de changement d'orbite, ces manœuvres étant qualifiées d'impulsionnelles, c’est-à-dire effectuées en un temps suffisamment bref pour que les hypothèses de l'équation de Tsiolkovski restent approximativement valables. Ainsi, pour effectuer une manœuvre requérant une variation de vitesse Δv à l'aide d'un propulseur caractérisé par une vitesse d'éjection des gaz v_e et un débit massique d'ergol q, l'équation de Tsiolkovski renseigne sur le temps d'allumage du moteur :

m₀ étant la masse de l'astronef préalablement à la manœuvre.

• Portail de la physique
• Portail de l’astronautique