- Vent thermique
-
 Pour les articles homonymes, voir Vent (homonymie).
Pour les articles homonymes, voir Vent (homonymie).Le vent thermique est un concept pratique en météorologie pour calculer la variation du vent entre deux altitudes quand on connaît la structure thermique de la masse d'air.
Sommaire
Définition
Dans l'atmosphère terrestre, le vent est dû à un équilibre entre différentes forces que sont le gradient de pression, la force de Coriolis, la gravité, la force centrifuge et la friction. À grande échelle, dite échelle synoptique, et suffisamment haut pour que la friction du terrain soit négligeable, la pression et Coriolis demeurent les seules forces dans l'équation. Il s'agit de l'équilibre géostrophique qui donne le vent géostrophique.
Le vent géostrophique selon les axes x et y à une altitude de (Z) de pression constante est donc[1] :
Selon cet équilibre, on utilise l'hypothèse hydrostatique et la loi des gaz parfaits pour calculer la relation entre la pression (p) et la température (T):
En combinant les deux, on obtient la relation qui donne le vent thermique (VT):
-
-
- Où:

- Où:
-
Formulation avec les températures
Si on prend une température moyenne dans la couche entre p0 et p1 comme
 , l'équation pour le vent thermique devient :
, l'équation pour le vent thermique devient :ou sous forme différentielle
Remarque:les différentiations étant à pression constante, on peut aussi écrire la formule en fonction de la température potentielle.
 Le vent thermique est donc perpendiculaire au gradient de T, avec les températures les plus basses à gauche dans l'hémisphère nord (à droite dans celle du sud).
Le vent thermique est donc perpendiculaire au gradient de T, avec les températures les plus basses à gauche dans l'hémisphère nord (à droite dans celle du sud).Formulation avec le géopotentiel
Ou si on transforme cette équation en utilisant le géopotentiel (
 ) :
) :- Erreur math (La conversion en PNG a échoué ; vérifiez l’installation de latex et dvipng (ou dvips + gs + convert)): \vec \mathbf{V}_T = \frac {\vec \mathbf{k} \times \vec \nabla ( \Phi_1 - \Phi_0 )} {f}
 Le vent thermique est donc perpendiculaire au gradient Φ, avec le géopotentiel le plus bas à gauche dans l'hémisphère nord (à droite dans celle du sud).
Le vent thermique est donc perpendiculaire au gradient Φ, avec le géopotentiel le plus bas à gauche dans l'hémisphère nord (à droite dans celle du sud).
Nota : Le vent thermique est indéterminé près de l'équateur puisque y est nul et que VT devient infini.
y est nul et que VT devient infini.Usage
Fronts et courant-jet
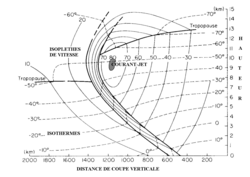 Coupe verticale des températures et des vents à travers un front. On remarque la bande de vents forts du courant-jet qui a est dû à la variation de température le long d'un front. Le vent thermique est le calcul de la variation du vent avec l'altitude dans le jet.
Coupe verticale des températures et des vents à travers un front. On remarque la bande de vents forts du courant-jet qui a est dû à la variation de température le long d'un front. Le vent thermique est le calcul de la variation du vent avec l'altitude dans le jet.
Selon la définition ci-dessus, une masse d'air où la variation de température avec l'altitude est la même partout n'aura aucun vent thermique. Le vent sera le même à toutes les altitudes, c'est ce qu'on appelle une masse d'air barotrope. Par contre, lorsqu'il y'a une variation de la température moyenne quand on se déplace selon x ou y, cela veut dire que le vent variera avec l'altitude et c'est alors une atmosphère barocline.
Dans la réalité, il y a généralement des contrastes thermiques dans l'atmosphère. En effet, les pôles et l'équateur ne sont pas réchauffés de la même façon par le Soleil à cause de l'angle d'incidence des rayons solaires. Comme les températures les plus froides sont aux pôles et les plus chaudes à l'équateur, le gradient de températures sera vers l'équateur. Par la définition du vent thermique, il va suivre la perpendiculaire à ce gradient (les isothermes) et être de direction générale d'ouest vers est. Cependant, la répartition de la chaleur n'est pas uniforme à cause des mouvements de l'air et le vent thermique se repère donc facilement sur une carte météorologique par les zones où la températures change rapidement: les zones frontales.
Dans ces zones, le vent change rapidement avec l'altitude et donne naissance au courant-jet. Cependant, à la tropopause, la température devient stable avant de réchauffer dans la stratosphère. Comme la tropopause est plus basse aux pôles qu'à l'équateur, le vent thermique change donc de direction à ce niveau car la température se réchauffe plus rapidement au nord ce qui inverse le gradient de température et donc le vent thermique. C'est ce qui forme le sommet du courant-jet.
Advection de température
Si le vent géostrophique tourne avec l'altitude, il transporte de l'air d'une certaine température depuis une zone vers une autre qui a une température différente. Il s'agit d'advection chaude ou froide selon le cas. Ceci change la distribution thermique et naturellement crée un vent thermique.
Une advection d'air chaud par le vent géostrophique va donc créer un gradient thermique perpendiculaire au vent et donc un vent thermique vers l'est ce qui cause une rotation dextrogyre des vents en altitude. L'inverse se produit pour une advection froide.
Bibliographie
- Holton, James R.: An Introduction to Dynamic Meteorology, 2004. (ISBN 0-12-354015-1)
- Vasquez, Tim: Weather Forecasting Handbook, 2002. (ISBN 0-9706840-2-9)
Notes
- Holton p. 68-71 où le géopotentiel Φ est transformé en Z
Voir aussi
Articles connexes
Liens externes
Catégories :- Théorie météorologique
- Mécanique des fluides
Wikimedia Foundation. 2010.



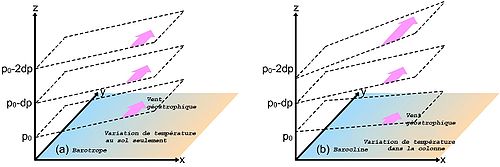
 est constant avec le changement de Z dans une atmosphère
est constant avec le changement de Z dans une atmosphère  )
) augmente avec Z dans une atmosphère
augmente avec Z dans une atmosphère  )
)

