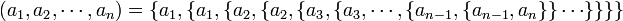Uple

Uple

N-uplet

En mathématiques, si n est un entier naturel non nul alors un n-uplet est une collection ordonnée de n objets. Les éléments sont aussi appelés composantes.

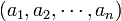Si nous notons a1 le premier élément, a2 le deuxième élément, ..., an le nème élément, le n-uplet s'écrit : (a_1, a_2, \cdots, a_n).

L'égalité des n-uplets se définit par

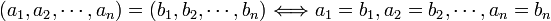(a_1,a_2,\cdots,a_n)=(b_1,b_2,\cdots,b_n) \Longleftrightarrow a_1=b_1, a_2=b_2, \cdots, a_n=b_n.

Un 2-uplet est un couple, un 3-uplet est un triplet, un 4-uplet est un quadruplet, un 5-uplet est un quintuplet, ...

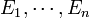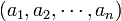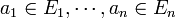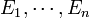Si E_1, \cdots, E_n sont des ensembles alors l'ensemble des n-uplets (a_1, a_2, \cdots, a_n), où a_1 \in E_1, \cdots, a_n \in E_n, est le produit cartésien des ensembles E_1, \cdots, E_n.

Sommaire

Exemples

Formalisation

Formellement, un n-uplet peut être défini en termes d'ensemble par

(a_1, a_2, \cdots, a_n) = \{a_1,\{a_1,\{a_2,\{a_2,\{a_3,\{a_3,\cdots,\{a_{n-1},\{a_{n-1},a_n\}\}\cdots\}\}\}\}

ou en utilisant une définition récursive :

  1. un 1-uplet (a1) est simplement a1;
  2. si x est un n-uplet, alors (x,an + 1) (i.e. {x,{x,an + 1}}) est un (n+1)-uplet.

Il est assez facile de démontrer que ces définitions sont équivalentes, cependant les ensembles obtenus sont très différents.

Programmation

Beaucoup de langages de programmation supportent les n-uplets comme type de donnée, formés aussi bien d'objets tous de même type ou d'objets de types différents.

Le langage de programmation LISP a utilisé dès ses débuts la notion abstraite de paire pour créer toutes ses structures de n-uplets et de listes, de manière similaire à la définition récursive précédente.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « N-uplet ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Uple de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • uple — non·uple; …   English syllables

  • N-uple — ● N uple ou N uplet nom masculin Élément du produit cartésien de n ensembles E1, E2, …, En (n ≥ 2). [Un n uple se note (a1, a2, …, an).] …   Encyclopédie Universelle

  • MODÈLES (THÉORIE DES) — «Modèle» est un terme qui appartient au vocabulaire de la plupart des sciences et qui a des significations multiples [cf. MODÈLE]. Ainsi, dans les sciences humaines, on entend généralement par modèle une théorie conçue pour expliquer un ensemble… …   Encyclopédie Universelle

  • RELATION — Le concept de relation apparaît comme l’un des concepts fondamentaux du discours rationnel. Il semble lié à la pratique de l’analyse, qui constitue elle même l’un des aspects essentiels de la démarche discursive. L’analyse décompose les unités… …   Encyclopédie Universelle

  • STATISTIQUE — Le mot «statistique» désigne à la fois un ensemble de données d’observation et l’activité qui consiste dans leur recueil, leur traitement et leur interprétation. Au cours de l’histoire, la collecte d’observations et la méthodologie de leur emploi …   Encyclopédie Universelle

  • Dependence logic — is a logical formalism, created by Jouko Väänänen[1], which adds dependence atoms to the language of first order logic. A dependence atom is an expression of the form , where are terms, and corresponds to the statement that the value of is… …   Wikipedia

  • COMBINATOIRE (ANALYSE) — L’analyse combinatoire est l’ensemble des techniques qui servent, en mathématiques, à compter (ou dénombrer ) certaines structures finies , ou à les énumérer (établir des listes exhaustives de structures considérées), enfin à démontrer leur… …   Encyclopédie Universelle

  • COURBES ALGÉBRIQUES — En fondant la géométrie analytique, Descartes avait substitué au plan de la géométrie d’Euclide l’ensemble R2 des couples de nombres réels et, de ce fait, à la notion de courbe, celle d’équation. La construction d’un point, puis la détermination… …   Encyclopédie Universelle

  • DÉCISION — La réflexion moderne sur la question de savoir quel parti prendre lorsqu’on se trouve confronté à un choix difficile a été esquissée pour la première fois par Blaise Pascal, au XVIIe siècle, dans le fameux texte du «pari» sur l’entrée dans la… …   Encyclopédie Universelle

  • SÉRIES ET PRODUITS INFINIS — La notion de limite d’une suite est à la base de l’analyse. Le langage des séries, équivalent à celui des suites, s’est imposé dès le XVIIe siècle à propos du développement des fonctions en série entière. Cependant, les fondements rigoureux de la …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”