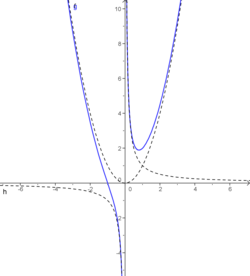
Trident de Newton

Trident d'équation y = x²+1/x

Le trident de Newton est le nom donné à une courbe étudiée par Isaac Newton. On la nomme aussi parfois parabole de Descartes - bien que ce ne soit pas une parabole.

Sommaire

1 Classification des cubiques
2 Équation cartésienne
3 Analyse
4 Intersection avec l'axe des abscisses
5 Lien avec le folium de Descartes
6 Voir aussi
- 6.1 Articles connexes
- 6.2 Liens externes

Classification des cubiques

Dans une étude menée en 1676 mais publiée en 1704, Newton cherche à classifier toutes les courbes cubiques, c’est-à-dire les courbes planes dont l'équation est de la forme :

$ax^3 + bx^2y + cxy^2 + dy^3 + ex^2 + fxy + gy^2 + hx + iy + j = 0\,$

Il en dénombre 72 types que l'ont peut ranger dans quatre classes par des changements de repère appropriés:

les courbes d'équation $x y 2 + e y = a x 3 + b x 2 + c x + d$
les courbes d'équation $x y = a x 3 + b x 2 + c x + d$
les courbes d'équation $y 2 = a x 3 + b x 2 + c x + d$
les courbes d'équation $y = a x 3 + b x 2 + c x + d$

Les tridents de Newton sont les courbes de type (2)

Équation cartésienne

Les tridents de Newton ont pour équation cartésienne canonique :

$x y = ax^3+ bx^2 + cx + d\,$

où a et d sont non nuls.

Analyse

Domaine de définition

Les tridents de Newton ne sont pas définis en 0. Leur domaine de définition est donc :

$D_f = \R^*$

Dérivée

Ce sont des fonctions rationnelles. Elles sont donc dérivables sur $D f$ , et leur dérivée est :

$f^'(x) = 2ax + b - \frac{d}{x^2}$

Limites

Limite en l'infini

En l'infini, les tridents de Newton tendent ou bien vers $+\infty$ , ou bien vers $-\infty$ .

Si a>0 alors $\lim_{x \to \pm\infty}f(x) = +\infty$ .

Si a<0 alors $\lim_{x \to \pm\infty}f(x) = -\infty$ .

Limites en 0

En 0, les tridents de Newton tendent vers $+\infty$ ou $-\infty$ .

Si d>0 alors $\lim_{x \to 0^+}f(x) = +\infty$ et $\lim_{x \to 0^-}f(x) = -\infty$ .

Si d<0 alors $\lim_{x \to 0^+}f(x) = -\infty$ et $\lim_{x \to 0^-}f(x) = +\infty$ .

Asymptotes

Ils ont pour asymptotes la parabole d'équation

y = a x 2 + b x + c

ainsi que l'hyperbole d'équation

$y = \frac{d}{x}$

Intersection avec l'axe des abscisses

On dénombre entre un et trois points d'intersection entre un trident de Newton et l'axe des abscisses selon la valeur des coefficients a, b, c, d.

Lien avec le folium de Descartes

Le changement de variable

$x = \frac XY$ et $y = \frac 1Y$

Conduit à une équation de la forme :

$XY = aX^3 + bX^2Y + cXY^2 + dY^3\,$

En particulier, la courbe d'équation $y = x^2 + \frac1x$ est alors transformée en un folium de Descartes

Voir aussi

Liens externes

(en) Liste de courbes connues
(en) Un applet Java de simulation de Tridents
(fr) Le trident de Newton (explications)
(en) Page sur les tridents
(en) Comparaison entre les tridents de Newton et ceux de Descartes

Portail de la géométrie

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Trident de Newton de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Trident de newton — Trident d équation y = x²+1/x Le trident de Newton est le nom donné à une courbe étudiée par Isaac Newton. On la nomme aussi parfois parabole de Descartes bien que ce ne soit pas une parabole. Sommaire … Wikipédia en Français
Trident curve — In mathematics, Trident curve (also trident of Newton or parabola of Descartes) is the name for a family of curves that have the formula::::xy+ax^3+bx^2+cx=dTrident curves are cubic plane curves with an ordinary double point in the real… … Wikipedia
Trident (gum) — Trident is a brand of sugarless chewing gum popular in the United States, United Kingdom, Canada, Australia, Greece, Guyana, Spain, Mexico, Portugal, Venezuela, Morocco, Thailand, Peru, Brazil, Ecuador and in Argentina Uruguay as Beldent . It was … Wikipedia
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Asymptote — Pour les articles homonymes, voir Asymptote (homonymie). Le terme d asymptote est utilisé en mathématiques pour préciser des propriétés éventuelles d une branche infinie de courbe à accroissement tendant vers l infinitésimal. C est d abord un… … Wikipédia en Français
Asymptote horizontale — Asymptote Pour les articles homonymes, voir Asymptote (homonymie). Le terme d asymptote est utilisé en mathématiques pour préciser des propriétés éventuelles d une branche infinie de courbe à accroissement tendant vers l infinitésimal. C est d… … Wikipédia en Français
Asymptote oblique — Asymptote Pour les articles homonymes, voir Asymptote (homonymie). Le terme d asymptote est utilisé en mathématiques pour préciser des propriétés éventuelles d une branche infinie de courbe à accroissement tendant vers l infinitésimal. C est d… … Wikipédia en Français
Asymptote verticale — Asymptote Pour les articles homonymes, voir Asymptote (homonymie). Le terme d asymptote est utilisé en mathématiques pour préciser des propriétés éventuelles d une branche infinie de courbe à accroissement tendant vers l infinitésimal. C est d… … Wikipédia en Français
Asymptotique — Asymptote Pour les articles homonymes, voir Asymptote (homonymie). Le terme d asymptote est utilisé en mathématiques pour préciser des propriétés éventuelles d une branche infinie de courbe à accroissement tendant vers l infinitésimal. C est d… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Trident de Newton

Sommaire

Classification des cubiques

Équation cartésienne