Transversalite

Transversalite

Transversalité

En algèbre linéaire et en géométrie différentielle, la propriété de transversalité est un qualificatif pour l'intersection de sous-espaces ou de sous-variétés. Elle est en quelque sorte l'opposé de la notion de tangence.

Deux sous-espaces vectoriels F, G d'un espace vectoriel E sont dits transverses quand F + G = E. Cette condition peut être réécrite, le cas échéant, en termes de codimension :

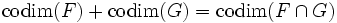\operatorname{codim}(F) + \operatorname{codim}(G)=\operatorname{codim} (F\cap G).

Deux sous-espaces affines Y, Z d'un espace affine X sont dites transverses si leurs directions sont transverses, c'est-à-dire si

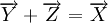\overrightarrow{Y}+\overrightarrow{Z}=\overrightarrow{X}.

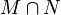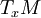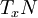Deux sous-variétés M et N d'une variété différentielle P sont dits transverses lorsque, pour tout point x de M\cap N, les espaces tangents \displaystyle T_xM et \displaystyle T_xN sont transverses dans l'espace tangent 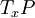\displaystyle T_xP, c'est-à-dire si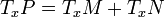

\displaystyle T_xP=T_xM + T_xN

Dans la suite, m,n,p désignent les dimensions respectives de M,N,P.

Remarques :

  • La définition reste valable pour les variétés banachiques.
  • Deux sous-variétés disjointes sont transverses.
  • Si m + n < p, alors la condition de transversalité ne peut être vérifiée seulement si les sous-variétés M et N sont disjointes.

Théorème — Une intersection transverse et non vide 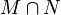M\cap N est une sous-variété différentielle de dimension m + n − p.

On a donc dans ce cas les relations

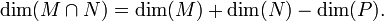
\operatorname{dim} (M\cap N) = \operatorname{dim}(M) + \operatorname{dim}(N)-\operatorname{dim}(P).
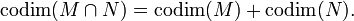
\operatorname{codim} (M\cap N) = \operatorname{codim}(M) + \operatorname{codim}(N).

Par exemple, deux surfaces régulières de l'espace à trois dimensions sont transverses si et seulement si elles n'ont aucun point de tangence. Dans ce cas, leur intersection forme une courbe régulière (éventuellement vide).

Nombre d'intersection

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Généricité

Théorème — Si M et N sont deux sous-variétés de classe Ck (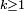\scriptstyle k\geq 1) de dimensions respectives m et n, alors il existe un Ck-difféomorphisme h de P, aussi proche de l'identité que souhaité en topologie Ck, tel que h(M) intersecte transversalement N.

En général, deux sous-variétés s'intersectent transversalement, quitte à perturber l'une d'elles par une isotopie.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Transversalit%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Transversalite de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • transversalité — ● transversalité nom féminin Caractère de ce qui est transversal …   Encyclopédie Universelle

  • Transversalité — En algèbre linéaire et en géométrie différentielle, la propriété de transversalité est un qualificatif pour l intersection de sous espaces ou de sous variétés. Elle est en quelque sorte l opposé de la notion de tangence. Deux sous espaces… …   Wikipédia en Français

  • transversalité — skersumas statusas T sritis fizika atitikmenys: angl. transversality vok. Transversalität, f rus. поперечность, f pranc. transversalité, f …   Fizikos terminų žodynas

  • Psychanalyse et transversalité — est un ouvrage de Félix Guattari, publié en 1974, dans lequel il expose sa réflexion sur les incidences de la psychanalyse, aussi bien dans le champ psychiatrique que dans le champ politique[1]. Références ↑ Présentation de l’éditeur actuel, La… …   Wikipédia en Français

  • condition de transversalité — skersumo sąlyga statusas T sritis fizika atitikmenys: angl. transversality condition vok. Transversalitätsbedingung, f rus. условие поперечности, n pranc. condition de transversalité, f …   Fizikos terminų žodynas

  • Intersection transverse — Transversalité En algèbre linéaire et en géométrie différentielle, la propriété de transversalité est un qualificatif pour l intersection de sous espaces ou de sous variétés. Elle est en quelque sorte l opposé de la notion de tangence. Deux sous… …   Wikipédia en Français

  • SINGULARITÉS DES FONCTIONS DIFFÉRENTIABLES (la théorie mathématique et ses applications) — De la topologie différentielle à la dynamique qualitative, en passant par la géométrie analytique et la topologie algébrique, les «singularités» ont bien des incarnations en mathématiques; mais cela n’exclut pas une certaine unité: qu’il s’agisse …   Encyclopédie Universelle

  • SYSTÈMES DYNAMIQUES DIFFÉRENTIABLES — Sans doute née avec le mémoire que Poincaré écrivit en 1881 «sur les courbes définies par des équations différentielles», où l’étude quantitative (analytique) locale des équations différentielles dans le champ complexe est remplacée par leur… …   Encyclopédie Universelle

  • Jacques Ardoino — Jacques Ardoino, né en 1927 à Paris, est un professeur français en sciences de l éducation à l Université de Paris VIII. Sommaire 1 Biographie 2 Un regard global 2.1 Transversalité …   Wikipédia en Français

  • TOPOLOGIE - Topologie différentielle — La topologie différentielle, que l’on devrait plutôt appeler «topologie des variétés », est une discipline mathématique assez ancienne par les problèmes qu’elle cherche à résoudre: ils étaient presque tous posés au début du siècle; mais ses… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”