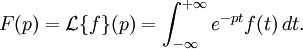Transformee bidirectionnelle de Laplace
- Transformee bidirectionnelle de Laplace
-
Transformée bidirectionnelle de Laplace
La transformée bilatérale de Laplace est une forme particulière de la transformée de Laplace, dans laquelle l'intégration se fait à partir de moins l'infini plutôt qu'à partir de zéro :
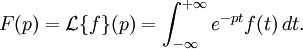
Elle a pour propriété de rendre les raisonnements mathématiques plus simple, moyennant quelques précautions supplémentaires car elle ne converge que si la fonction à laquelle on l'applique tend rapidement[1] vers zéro pour les valeurs d'abscisses négatives.
Elle est utilisée, entre autres par certains automaticiens[2] et en statistiques où elle définit la fonction génératrice des moments d'une distribution.
Notes et références
- ↑ i.e. plus rapidement qu'une fonction exponentielle
- ↑ Raymond Hanus & Philippe Bogaerts, Introduction à l'automatique - vol 1. Système continus, De Boek Université, 1996
 Portail des mathématiques
Portail des mathématiques
Catégories : Transformée | Analyse fonctionnelle
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Transformee bidirectionnelle de Laplace de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Transformée bidirectionnelle de Laplace — La transformée bilatérale de Laplace est une forme particulière de la transformée de Laplace, dans laquelle l intégration se fait à partir de moins l infini plutôt qu à partir de zéro : Elle a pour propriété de rendre les raisonnements… … Wikipédia en Français
Transformée — En mathématiques, une transformée consiste à associer une fonction à une autre fonction. Liste des transformées Transformée de Fourier Transformée de Fourier discrète Transformée de Fourier rapide Transformée de Fourier locale Transformée de… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Machine a courant continu — Machine à courant continu Une machine à courant continu est une machine électrique. Il s agit d un convertisseur électromécanique permettant la conversion bidirectionnelle d énergie entre une installation électrique parcourue par un courant… … Wikipédia en Français
Machine À Courant Continu — Une machine à courant continu est une machine électrique. Il s agit d un convertisseur électromécanique permettant la conversion bidirectionnelle d énergie entre une installation électrique parcourue par un courant continu et un dispositif… … Wikipédia en Français
Machine à courant continu — Une machine à courant continu est une machine électrique. Il s agit d un convertisseur électromécanique permettant la conversion bidirectionnelle d énergie entre une installation électrique parcourue par un courant continu et un dispositif… … Wikipédia en Français
Moteur à courant continu — Machine à courant continu Une machine à courant continu est une machine électrique. Il s agit d un convertisseur électromécanique permettant la conversion bidirectionnelle d énergie entre une installation électrique parcourue par un courant… … Wikipédia en Français
Moteurs à courant continu — Machine à courant continu Une machine à courant continu est une machine électrique. Il s agit d un convertisseur électromécanique permettant la conversion bidirectionnelle d énergie entre une installation électrique parcourue par un courant… … Wikipédia en Français
Moteurs à courant continus — Machine à courant continu Une machine à courant continu est une machine électrique. Il s agit d un convertisseur électromécanique permettant la conversion bidirectionnelle d énergie entre une installation électrique parcourue par un courant… … Wikipédia en Français