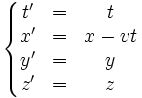Transformation de Galilée

Transformation de Galilée

Transformations de Galilée

Les transformations de Galilée désignent le groupe de transformations qui permet de lier deux systèmes de coordonnées de deux référentiels galiléens, c'est-à-dire en mouvement relatif uniforme en mécanique newtonienne.

Soient (x, y, z, t) les coordonnées d'un point dans un référentiel A, et (x', y', z', t') les coordonnées de ce point dans le référentiel A'. Si A' est en mouvement uniforme de vitesse v dans la direction x, relativement à A, alors on a :

\left\{\begin{matrix} t'&=&t\\ x'&=&x - vt\\ y'&=&y\\ z'&=&z \end{matrix}\right.

Ces équations de la transformation sont le cas particulier (et beaucoup plus simple) des transformations de Lorentz où le paramètre c, la vitesse de la lumière, serait infinie. On sait que ce n'est pas le cas, mais elles restent suffisamment bonnes (et, par conséquent, la mécanique newtonienne reste valable) tant que la vitesse relative des référentiels est assez petite par rapport à la vitesse de la lumière. Sinon, il faut revenir au groupe des transformations de Lorentz et adopter la relativité restreinte.

Voir aussi

  • Portail de la physique Portail de la physique
Ce document provient de « Transformations de Galil%C3%A9e ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Transformation de Galilée de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Transformation de Galilee — Transformations de Galilée Les transformations de Galilée désignent le groupe de transformations qui permet de lier deux systèmes de coordonnées de deux référentiels galiléens, c est à dire en mouvement relatif uniforme en mécanique newtonienne.… …   Wikipédia en Français

  • formule de transformation de Galilée — Galilėjaus transformacijos formulė statusas T sritis fizika atitikmenys: angl. Galileo transformation law vok. Galileische Transformationsformel, f rus. формула трансформации Галилея, f pranc. formule de transformation de Galilée, f …   Fizikos terminų žodynas

  • Transformation de lorentz — Cet article présente les transformations de Lorentz sous un aspect technique. Le lecteur désireux d obtenir des informations physiques plus générales à ce sujet pourra se référer à l article relativité restreinte. Les transformations de Lorentz… …   Wikipédia en Français

  • Transformation de Lorentz — Cet article présente les transformations de Lorentz sous un aspect technique. Le lecteur désireux d obtenir des informations physiques plus générales à ce sujet pourra se référer à l article relativité restreinte. Hendrik Antoon Lorentz en 1916… …   Wikipédia en Français

  • Transformation galiléenne — Transformations de Galilée Les transformations de Galilée désignent le groupe de transformations qui permet de lier deux systèmes de coordonnées de deux référentiels galiléens, c est à dire en mouvement relatif uniforme en mécanique newtonienne.… …   Wikipédia en Français

  • Galileo transformation law — Galilėjaus transformacijos formulė statusas T sritis fizika atitikmenys: angl. Galileo transformation law vok. Galileische Transformationsformel, f rus. формула трансформации Галилея, f pranc. formule de transformation de Galilée, f …   Fizikos terminų žodynas

  • New Galilee (Sixth Epoch) — The New Galilee is the name given in the Western Wisdom Teachings to the New Jerusalem mentioned in the Bible. According to these Christian esoteric teachings, the New Galilee represents the future Sixth Epoch in mankind s evolutionary path and… …   Wikipedia

  • Interactions Transformation Personnelle — Transformation Sociale (Interactions TP TS) est le nom d’un projet de dimension politique qui affirme que la question de la qualité des relations entre les citoyens est une question politique à part entière qui doit être intégrée avec conscience… …   Wikipédia en Français

  • Transformations de Galilee — Transformations de Galilée Les transformations de Galilée désignent le groupe de transformations qui permet de lier deux systèmes de coordonnées de deux référentiels galiléens, c est à dire en mouvement relatif uniforme en mécanique newtonienne.… …   Wikipédia en Français

  • Transformations de galilée — Les transformations de Galilée désignent le groupe de transformations qui permet de lier deux systèmes de coordonnées de deux référentiels galiléens, c est à dire en mouvement relatif uniforme en mécanique newtonienne. Soient (x, y, z, t) les… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”