Tractrice

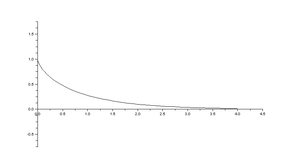
Tractrice pour x et y positifs, T parcourt [Ox)

En mathématique, une tractrice est une courbe plane parcourue par un point M lié à un point T par les conditions suivantes :

le point T parcourt une droite
la distance MT est fixe
la droite (MT) est tangente à la tractrice

L'histoire de la tractrice remonte au XVII^esiècle. Claude Perrault rencontrant Leibniz vers les années 1670 lui aurait parlé d'un problème qu'il aurait posé déjà à de nombreux mathématiciens sans en obtenir de réponse satisfaisante. Posant sa montre à gousset sur la table, il la tire par la chaînette en suivant avec l'extrémité de la chaînette une trajectoire rectiligne et demande quelle est la trajectoire suivie par la montre. Nous sommes alors au tout début du calcul infinitésimal et des équations différentielles. Leibniz propose une mise en équation mais la résolution proprement dite demande l'outil des fonctions logarithmes ou des fonctions hyperboliques. De nombreux autres mathématiciens s'intéressent alors à cette courbe et proposent même des instruments permettant la construction mécanique d'une tractrice. On peut imaginer une construction de la tractrice à l'aide d'une adaptation de la méthode d'Euler.

Propriétés

La tractrice est une développante de la chaînette.
Elle admet l'axe des abscisses comme asymptote.
On l'appelle parfois courbe aux tangentes égales pour exprimer que la longueur des segments de tangentes limités à la courbe et à l'asymtote est constante.

Construction graphique

Pour construire une approximation d'une tractice entre les points M₁ et M₂ associés aux points T₁ et T₂, on divise le segment [T₁T₂] en n intervalles [t_it_i+1] qui permettent de construire n+1 points m₀, ..., m_n de la tractrice (m₀ = M₁ et m_n = M₂) de proche en proche. Si r est la distance M₁T₁, on trace le segment [m_it_i+1] et on place le point m_i+1 sur ce segment et à une distance r de t_i+1.

Résolution mathématique

Tractrice, position de M et T

En considérant la tractrice comme une courbe paramétrée, autrement dit si (x(t), y(t)) sont les coordonnées cartésiennes de M dans un repère orthonormé, cherchons deux fonctions x et y vérifiant x(0) = 0, y(0) = a et vérifiant les conditions requises.

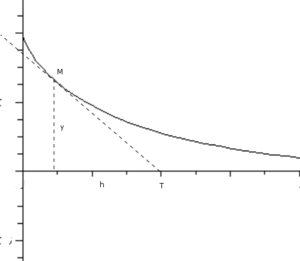
Dans le dessin ci-contre, elles se traduisent par

$y 2 + h 2 = a 2$ pour MT = a
(h ; -y) est proportionnel à (x' ; y') car (MT) est tangente à la courbe.

Le problème revient donc à résoudre la relation différentielle :

$y^2 + \left(\frac{x'y}{y'}\right)^2 = a^2$

dans laquelle il s'agit de choisir judicieusement les fonctions paramétrées.

y en fonction de x

En prenant x comme paramètre, on obtient l'équation

$y'^2 = \frac{y^2}{a^2-y^2}$

Soit encore

$y' = \pm\frac{y}{\sqrt{a^2-y^2}}$

C'est une équation différentielle autonome. Cela était prévisible puisque la propriété géométrique étudiée est invariante par translation parallèle à l'axe des x : si le graphe $x\mapsto y(x)$ a la propriété requise, il doit en être de même du graphe de $x\mapsto y(x-x_0)$ , quel que soit le réel $x 0$ .

Pour une telle équation, sur tout intervalle où $y^\prime$ ne s'annule pas, on peut expliciter les fonctions réciproques des solutions au moyen d'intégrales. Ici, pour les conditions initiales requises,

$x=\int_a^y\pm\frac{\sqrt{a^2-u^2}}{u}du$

Cette intégrale peut se calculer par exemple avec le changement de variable $u = a cos t$ . Cela revient à employer la méthode du paragraphe suivant.

Avec des fonctions trigonométriques

Si on se limite aux conditions x et y positifs ou nuls, avec comme conditions initiales x ₀ = 0 et y ₀ = a on peut poser

$y = a \cos(t)\,$ avec $t \in [0; \pi/2[$ (la géométrie du problème imposant la condition

$0\le y\le a$ .

L'équation devient (

$a^2\cos^2(t) + x'^2(t)\frac{cos^2(t)}{1-cos^2(t)}= a^2$

cette équation devient, après avoir isolé x'

$x'(t) = a\frac{1-\cos^2(t)}{\cos(t)}$

$x'(t) = a\left(\frac{1}{\cos(t)}- \cos(t)\right)$

En posant u(t) = sin(t), on obtient

$x'(t) = a\left(\frac{u'(t)}{1 - u^2(t)}- u'(t)\right)$

Qui s'intègre en

$x(t) = a\left((\frac{1}{2}\ln\left(\frac{1+u(t)}{1 - u(t)}\right) - u(t)\right)$

Donc

$x(t) = a\left(\ln\left(\frac{1+\sin(t)}{\cos(t)}\right) - \sin(t)\right)$

Puis, en remplaçant acos(t) par y

$x = a\ln\left(\frac{a + \sqrt{a^2-y^2}}{y}\right) - \sqrt{a^2-y^2}$

Avec des fonctions hyperboliques

Si on se limite aux conditions x et y positifs ou nuls, avec comme conditions initiales x ₀ = 0 et y ₀ = a on peut poser

$y = \frac{a}{cosh(t)}$

L'équation devient alors

$\frac{a^2}{\cosh^2(t)} + x'^2(t)\frac{\cosh^2(t)}{\sinh^2(t)}=a^2$

et après avoir isolé x'

$x'(t) = a\frac{\sinh^2(t)}{\cosh^2(t)}= a\left(1-\frac{1}{\cosh^2(t)}\right)$

qui s'intègre en

$x(t) = a(t - \tanh(t))\,$

Quelques remarques

La relation entre ces deux point de vue

est donnée par la fonction de Gudermann.

la surface de révolution obtenue en faisant tourner la tractrice autour de son asympote

est la pseudo-sphère de Beltrami. Cette surface qui est localement isométrique au Demi-plan de Poincaré, fut le premier modèle explicite de la géométrie de Lobatchevski.

Voir aussi

Sur les autres projets Wikimedia :

« Tractrice », sur Wikimedia Commons (ressources multimédia)

Tractoire
Histoire de la tractrice
Tractrice sur le site de Serge Mehl

Portail de la géométrie

Catégorie :

Courbe

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Tractrice de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

tractrice — TRACTRÍCE s.f. (mat.) Curbă plană având proprietatea că, în fiecare punct al ei, segmentul de tangentă, cuprins între punctul de tangentă şi intersecţia tangentei cu o dreaptă fixă, are lungimea constantă. [< germ. Traktrix, cf. lat. tractare… … Dicționar Român
tractrice — ● tracteur, tractrice adjectif (latin tractum, de trahere, tirer) Qui tracte, qui est capable de tracter. Se dit de la force d un courant, qui lui permet d attaquer le fond et les berges et de transporter des matériaux solides. tractrice… … Encyclopédie Universelle
tracteur — 1. tracteur [ traktɶr ] n. m. • 1876; du lat. tractum, supin de trahere « tirer » ♦ Véhicule automobile (originairement, à vapeur) destiné à tirer un ou plusieurs véhicules, en particulier des remorques ou des engins roulants (tracteurs d… … Encyclopédie Universelle
Tractrix — (from the Latin verb trahere pull, drag ), or tractrice, is the curve along which a small object moves, under the influence of friction, when pulled on a horizontal plane by a piece of thread and a puller that moves at a right angle to the… … Wikipedia
tractoire — ⇒TRACTOIRE, adj. et subst. fém. I. Adjectif A. HYDROL. Force tractoire. Synon. de force tractrice (v. tracteur I B). (Dict. XXe s.). B. MÉCAN. [Corresp. à traction B] Relatif à la traction. Machine tractoire (Dict. XXe s.). II. Subst. fém., GÉOM … Encyclopédie Universelle
Musique électrique — Sonorisation Pour les articles homonymes, voir sonorisation (homonymie). La sonorisation englobe diverses techniques visant à la gestion des sons dans un lieu, cela passe généralement par un renforcement d une ou plusieurs sources sonores… … Wikipédia en Français
Sonorisateur — Sonorisation Pour les articles homonymes, voir sonorisation (homonymie). La sonorisation englobe diverses techniques visant à la gestion des sons dans un lieu, cela passe généralement par un renforcement d une ou plusieurs sources sonores… … Wikipédia en Français
Sonorisation — Pour les articles homonymes, voir sonorisation (homonymie). Complexe et puissant système de sonorisation utilisé pour un grand concert en plein air. La sonorisation est l ensemble des moyens permetta … Wikipédia en Français
Tractoire — En mathématiques, les tractoires sont des courbes planes dont le processus de construction est apparenté à celui de la tractrice. Les tractoires constituent des moyens géométriques pour résoudre des équations différentielles. Le mathématicien… … Wikipédia en Français
1692 en science — Années : 1689 1690 1691 1692 1693 1694 1695 Décennies : 1660 1670 1680 1690 1700 1710 1720 Siècles : XVIe siècle XVIIe sièc … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Tractrice

Sommaire

Propriétés

Construction graphique