- Théorème de sard
-
Théorème de Sard
Le théorème de Sard, connu aussi sous le nom de lemme de Sard ou théorème de Morse-Sard, est un résultat de mathématiques qui donne des informations sur l'image K de l'ensemble des point critique d'une fonction fonction lisse F d'un espace euclidien vers un autre. L'ensemble K a alors une mesure de Lebesgue nulle.
Sommaire
Énoncé
On considère une fonction f définie sur un ouvert U de
, à valeurs dans 
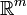, et de classe Cr.On appelle points critiques les points pour lesquelles l'application différentielle de f est non surjective, et valeurs critiques les images des points critiques. Les valeurs non critiques sont dites régulières (qu'elles soient des valeurs effectivement prises par f ou non).
Avec ces notations, le théorème de Sard s'énonce
- si r > max(0,n − m), alors l'ensemble des valeurs critiques a une mesure de Lebesgue nulle.
En revanche, l'ensemble des points critiques peut être très important, par exemple si n < m, tous les points sont critiques, mais l'ensemble image de f sera quand même de mesure nulle.
Il résulte notamment du théorème que l'ensemble des valeurs régulières est dense dans
, un fait déjà prouvé par A. Brown en 1935[1], d'où le nom de théorème de densité de Sard (ou de Sard-Brown) parfois donné au théorème[2].Le cas m = 1 a été prouvé par A. P. Morse en 1939[3], et le cas général par Arthur Sard en 1942[4]. Une version pour les espaces de Banach de dimension infinie a été prouvée par Stephen Smale[5].
Notes
- ↑ (en) A. Brown, Functional dependance, Trans. Amer. Math. Soc. 38, 1935, p379-394
- ↑ « The theorem of Sard and Brown » chez Milnor, « Sard's density theorem » pour Abraham-Robbin
- ↑ (en) A. P. Morse, The behavior of a function on its critical set, Ann. Math. 40 (1939), p. 62-70
- ↑ (en) A. Sard, The measure of the critical values of differentiable maps, Bull. Amer. Math. Soc. 48 (1942), p. 883-890
- ↑ (en) S. Smale, An infinite dimensional version of Sard's theorem, Amer. J. Math. 87 (1965), p 861-866
Voir aussi
Articles connexes
Références
- (en) John Milnor, Topology from the Differentiable Viewpoint [détail des éditions]
- (en) Ralph Abraham, Joel Robbin, Transversal mappings and flows [détail des éditions]
Portail des mathématiques
Catégories : Théorie de la mesure | Théorème d'analyse
Wikimedia Foundation. 2010.
