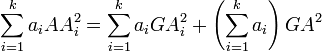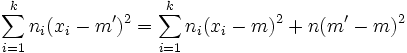Théorème de könig-huyghens

Théorème de König-Huyghens

En statistiques et en théorie des probabilités, le théorème de König-Huygens est une identité remarquable reliant la variance et la moyenne.

Sommaire

1 Énoncé en probabilités
2 Énoncé en statistiques
- 2.1 Généralisation
- 2.2 Relation avec la fonction de Leibniz
3 Énoncé en mécanique (Théorème d'Huygens)
4 Références

Énoncé en probabilités

Le théorème de König-Huygens énonce de la façon suivante :

Théorème — Pour toute variable aléatoire réelle $X$ , on a :

$\operatorname{Var}(X)\equiv E\bigl[(X-E[X])^2\bigr]=E[X^2]-E[X]^2$ .

La démonstration est relativement simple et algébrique. Trois points sont à rappeler :

Le développement du binôme de Newton ;
La linéarité de l'espérance en fonction de la variable aléatoire ;
L'espérance d'une constante vaut cette constante.

Ces trois propriétés rappelées impliquent :

$E\bigl[(X-E[X])^2\bigr]=E[X^2]-2E[X]E[X]+E[X]^2$ .

Énoncé en statistiques

Ce théorème peut également s'appliquer pour une décomposition de la formule de la variance empirique:

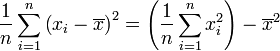Théorème — $\frac{1}{n} \sum_{i=1}^n \left( x_i - \overline{x}\right)^2 = \left(\frac{1}{n}\sum_{i=1}^n x_i^2\right) - \overline{x}^2$

Démonstration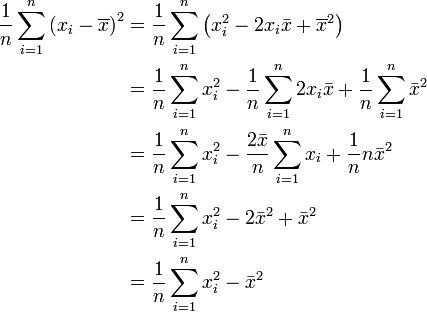

$\begin{align} \frac{1}{n} \sum_{i=1}^n \left( x_i - \overline{x}\right)^2 &= \frac{1}{n} \sum_{i=1}^n \left( x_i^2 -2x_i\bar x +\overline{x}^2\right)&\\ &= \frac{1}{n} \sum_{i=1}^n x_i^2 -\frac{1}{n} \sum_{i=1}^n 2x_i\bar x +\frac{1}{n} \sum_{i=1}^n\bar{x}^2\\ &= \frac{1}{n} \sum_{i=1}^n x_i^2 -\frac{2\bar x}{n} \sum_{i=1}^n x_i +\frac{1}{n} n\bar{x}^2\\ &= \frac{1}{n} \sum_{i=1}^n x_i^2 -2\bar x^2 +\bar{x}^2\\ &= \frac{1}{n} \sum_{i=1}^n x_i^2 -\bar{x}^2\\ \end{align}$

Généralisation

Cette formulation est un fait un cas particulier d'une identité plus générale:

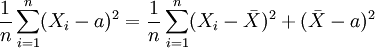Identité — $\frac{1}{n}\sum_{i=1}^n(X_i-a)^2=\frac{1}{n}\sum_{i=1}^n(X_i -\bar X)^2+(\bar X -a)^2$

Démonstration

$\begin{align} \sum_{i=1}^n(X_i-a)^2 &=\sum_{i=1}^n(X_i-\bar X+\bar X -a)^2\\ &=\sum_{i=1}^n\left((X_i-\bar X)+(\bar X -a)\right)^2\\ &=\sum_{i=1}^n\left[(X_i-\bar X)^2+2(X_i-\bar X)(\bar X-a)+(\bar X -a)^2\right]\\ &=\sum (X_i-\bar X)^2 +2(\bar X-a)(\sum X_i-\bar X)+n(\bar X -a)^2\\ &=\sum (X_i-\bar X)^2 +2(\bar X-a)(\sum X_i-n\frac{1}{n}X_i)+n(\bar X -a)^2\\ &=\sum_{i=1}^n(X_i -\bar X)^2+n(\bar X -a)^2 \end{align}$

NB: la démonstration est tirée de Mood et al. (2001, p. 229)

Remarque :

En passant le deuxième terme de droite à gauche et en prenant a=0 on retrouve la formule de la variance montrée plus haut:

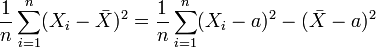
$\frac{1}{n}\sum_{i=1}^n(X_i -\bar X)^2=\frac{1}{n}\sum_{i=1}^n(X_i-a)^2-(\bar X -a)^2$

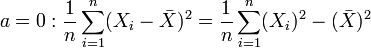
Et donc si $a=0: \frac{1}{n}\sum_{i=1}^n(X_i -\bar X)^2=\frac{1}{n}\sum_{i=1}^n(X_i)^2-(\bar X)^2$

Relation avec la fonction de Leibniz

Ce théorème est un cas particulier de simplification de la fonction scalaire de Leibniz concernant des barycentres.

En effet, la moyenne $m$ est le barycentre du système pondéré ${(x i, n i)} i = 1... k$ . La simplification de la fonction scalaire de Leibniz donne pour le système ${(A i, a i) i = 1... k}$ de barycentre $G$ :

$\sum_{i = 1}^k a_i AA_i^2 = \sum_{i = 1}^k a_i GA_i^2 +\left( \sum_{i = 1}^k a_i\right) GA^2$

En remplaçant $G$ par $m$ , $M$ par $m'$ , $a i$ par $n i$ et $A i$ par $x i$ , on obtient

$\sum_{i = 1}^k n_i (x_i - m')^2 = \sum_{i = 1}^k n_i (x_i - m)^2 + n (m' - m)^2$

Ce qui est, à un facteur $n$ près et à l'ordre près, la formule précédente.

Énoncé en mécanique (Théorème d'Huygens)

Soit un système de $k$ points matériels $A i$ , de masse respective $m i$ , de masse totale $M$ , de centre de masse $G$ et un point $A$ distant de $d$ du point $G$ . Le théorème de transport ou théorème de Huygens ou théorème de Steiner donne $J A$ le moment d'inertie du système par rapport à $A$ en fonction de $J G$ le moment d'inertie du système par rapport à $G$ :

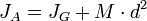
$J_A=J_G+M\cdot d^2$

avec

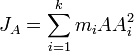
$J_A=\sum_{i = 1}^k m_i AA_i^2$

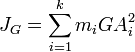
$J_G=\sum_{i = 1}^k m_i GA_i^2$

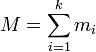
$M=\sum_{i = 1}^k m_i$

$d 2 = G A 2$

Références

(en) Alexander MacFarlane Mood, Introduction to the Theory of Statistics, Tata McGraw-Hill, New Delhi (ISBN 0070428646), p. 564

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de K%C3%B6nig-Huyghens ».

Catégories : Statistiques | Probabilités | Théorème de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de könig-huyghens de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Theoreme de Konig-Huyghens — Théorème de König Huyghens En statistiques et en théorie des probabilités, le théorème de König Huygens est une identité remarquable reliant la variance et la moyenne. Sommaire 1 Énoncé en probabilités 2 Énoncé en statistiques … Wikipédia en Français
Théorème de König-Huyghens — Pour les articles homonymes, voir Théorème de König. En statistiques et en théorie des probabilités, le théorème de König Huygens est une identité remarquable reliant la variance et la moyenne. Sommaire 1 Énoncé en probabilité … Wikipédia en Français
Théorème de Koenig-Huyghens — Théorème de König Huyghens En statistiques et en théorie des probabilités, le théorème de König Huygens est une identité remarquable reliant la variance et la moyenne. Sommaire 1 Énoncé en probabilités 2 Énoncé en statistiques … Wikipédia en Français
Theoreme de Konig — Théorème de König Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Il existe plusieurs « théorèmes de König » pour la simple raison qu il existe plusieurs scientifiques portant le nom de König… … Wikipédia en Français
Théorème de könig — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Il existe plusieurs « théorèmes de König » pour la simple raison qu il existe plusieurs scientifiques portant le nom de König (que l on… … Wikipédia en Français
Théorème de König — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Il existe plusieurs « Théorèmes de König » pour la simple raison qu il existe plusieurs scientifiques portant le nom de König (écrit aussi… … Wikipédia en Français
Théorème de Koenig-Huygens — Théorème de König Huyghens En statistiques et en théorie des probabilités, le théorème de König Huygens est une identité remarquable reliant la variance et la moyenne. Sommaire 1 Énoncé en probabilités 2 Énoncé en statistiques … Wikipédia en Français
Théorème de Koenig — Théorème de König Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Il existe plusieurs « théorèmes de König » pour la simple raison qu il existe plusieurs scientifiques portant le nom de König… … Wikipédia en Français
Théorèmes de König — Théorème de König Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Il existe plusieurs « théorèmes de König » pour la simple raison qu il existe plusieurs scientifiques portant le nom de König… … Wikipédia en Français
Johann Samuel König — Pour les articles homonymes, voir König. Johann Samuel König Naissance 31 juillet 1712 Büdingen (Allemagne) Décès 21 août 1757 (à 45 … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de könig-huyghens