- Théorème de heine
-
Théorème de Heine
Le théorème de Heine, nommé ainsi en l'honneur de Édouard Heine, s'énonce ainsi : Soit deux espaces métriques X et Y, tel que X soit également compact. Alors toute application continue de X dans Y est uniformément continue. Cela implique notamment que toute fonction continue de [a,b] dans
 est uniformément continue sur [a,b].
est uniformément continue sur [a,b].Sommaire
Énoncé et démonstration pour les fonctions numériques
Énoncé
Soit une fonction f de [a,b] dans
 , continue sur le segment [a,b]. Alors, f est uniformément continue sur ce segment.
, continue sur le segment [a,b]. Alors, f est uniformément continue sur ce segment.Utilisation
f étant continue en tout point x, nous savons donc que :
![\forall x \in [a,b], \forall \epsilon > 0, \exists \alpha_{x,\epsilon} > 0](/pictures/frwiki/98/bdfc26e10a12c2b376c1a070a9adb16a.png) tel que
tel que ![\forall y \in [a,b], |x-y|<\alpha_{x,\epsilon} \Rightarrow |f(x)-f(y)|<\epsilon](/pictures/frwiki/98/bfad44cb03e07b47e6b9f8384328290b.png) .
.Le théorème de Heine permet donc d'affirmer qu'elle est uniformément continue sur le segment [a,b], c'est à dire que le α peut être choisi indépendamment de x, ce qui nous permet d'inverser les deux quantificateurs :
![\forall x \in [a,b], \exists \alpha_x](/pictures/frwiki/99/c6c201d426d6bb94550a4d8c3fd62e5e.png) en
en ![\exists \alpha, \forall x \in [a,b]](/pictures/frwiki/98/b97ca2007f9c8899bb608b1dcaeafdd7.png) .
.La propriété d'uniforme continuité s'exprime alors :
 tel que
tel que ![\forall x \in [a,b], \forall y \in [a,b], |x-y|<\alpha_\epsilon \Rightarrow |f(x)-f(y)|<\epsilon](/pictures/frwiki/52/4af3274411e3a7b135b47c2fba0a35f2.png) .
.Démonstration
Fixons un ε > 0 et posons, pour tout
![x\in[a,b]](/pictures/frwiki/56/8290bddba5acf9822dcbf61f4ac67d1b.png) ,
, 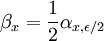 (où les αx,ε / 2 sont ceux liés à la continuité de f). Considérons
(où les αx,ε / 2 sont ceux liés à la continuité de f). Considérons ![[a,b]=\cup_{x\in[a,b]} \{x\} \subset \cup_{x\in[a,b]} B(x,\beta_x)](/pictures/frwiki/52/448083f6d93d46b4a2df875090edb80a.png) . C'est un recouvrement de [a,b] par des ouverts donc (d'après le Théorème de Borel-Lebesgue) on peut en extraire un sous-recouvrement fini :
. C'est un recouvrement de [a,b] par des ouverts donc (d'après le Théorème de Borel-Lebesgue) on peut en extraire un sous-recouvrement fini : ![[a,b]\subset\cup_{z\in Z}B(z,\beta_z)](/pictures/frwiki/101/e20cd313a6913c3320261cb8890cbc10.png) pour une certaine partie finie Z de [a,b].
pour une certaine partie finie Z de [a,b].Posons
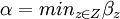 . Alors, pour tous
. Alors, pour tous ![x,y\in[a,b]](/pictures/frwiki/99/cb79e328f847e7458950b6147a06dbba.png) tels que | x − y | < α, en choisissant un
tels que | x − y | < α, en choisissant un 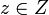 tel que
tel que 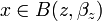 on obtient | x − z | < βz et
on obtient | x − z | < βz et 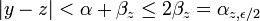 , donc
, donc .
.La valeur α trouvée étant bien indépendante de x, l'uniforme continuité est démontrée.
Démonstration dans le cas général en utilisant la propriété de Bolzano-Weierstrass
On se place dans le cas général de deux espaces métriques X et Y avec X compact. On note d la distance sur X et d' la distance sur Y. Le théorème de Heine nous dit alors toute application continue de X dans Y est uniformément continue, ce qui s'exprime par :
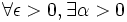 tel que
tel que 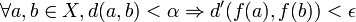 .
.Pour montrer cela, on peut reproduire la démonstration précédente en remplaçant simplement [a,b] par X,
 par Y, Théorème de Borel-Lebesgue par définition de la compacité (ou même directement par précompacité), et valeur absolue de la différence par distance.
par Y, Théorème de Borel-Lebesgue par définition de la compacité (ou même directement par précompacité), et valeur absolue de la différence par distance.Une autre méthode est de raisonner par contraposée en supposant f non uniformément continue sur X et en prouvant qu'elle n'est alors pas continue sur X. Par hypothèse, il existe ε > 0 tel que pour chaque α > 0, l'implication
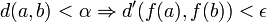 soit fausse pour certains a,b, en particulier tel que pour chaque
soit fausse pour certains a,b, en particulier tel que pour chaque 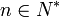 , il existe deux points an et bn de X tels que
, il existe deux points an et bn de X tels que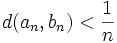 et
et 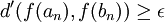 .
.La suite (an) est à valeurs dans le compact X donc on peut en extraire une sous-suite convergente. On note
 l'extraction et a la limite de la sous-suite. La relation
l'extraction et a la limite de la sous-suite. La relation 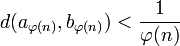 montre que
montre que 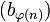 converge aussi vers a. Il s'ensuit que pour tout η > 0, il existe
converge aussi vers a. Il s'ensuit que pour tout η > 0, il existe 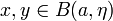 tels que
tels que 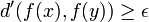 donc tels que
donc tels que  ou
ou 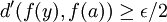 , ce qui prouve la non continuité de f au point a.
, ce qui prouve la non continuité de f au point a.Voir aussi
- Portail des mathématiques
Catégories : Compacité | Théorème de topologie
Wikimedia Foundation. 2010.
